Tiago Charters work blog gallery about contact

Sphere anemometers are simple devices that use the wind drag force on a sphere to determine the wind speed by equating the weight of the sphere with the drag force in a pendulum like configuration.

The drag force is the force that a sphere feels when traveling with a certain speed 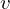in a viscous fluid (relatively to the fluid, in our case air). This forces depends on the relative velocity between the air and the sphere, on the density of the air 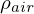, effective area in contact with the fluid 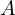and an adimensional coefficient 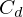called the drag coefficient. In this case this force amounts to

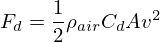
Note that the drag coefficient 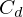is a geometric factor and is usually determined experimentally. For a sphere, for high enough Reynolds numbers, the drag coefficient is around 0.5.

Apparently this kind of anemometer was invented in 1900 by G. Daloz. Modern versions includes a ping-pong ball.

Equating the weight of the sphere

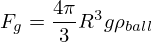
with the drag force in a pendulum like configuration for a given equilibrium position one gets

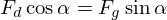
and for the velocity:

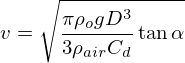Where D=2 R is the diameter of the ping-pong ball.

Given that a ping-pong ball has mass of 2.7g and a typical diameter of 40mm one gets for the density rhoball=2.7/(4*pi/3*2^3)~0.081 g/cm^3

and thus

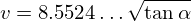
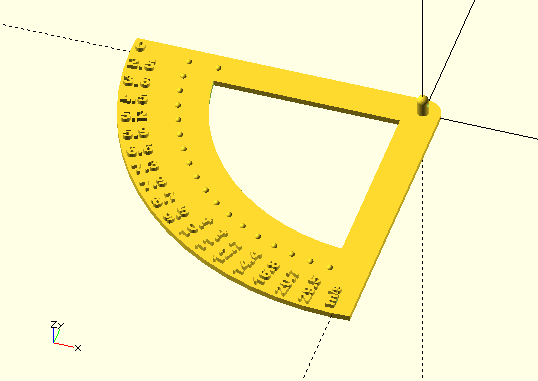
Here's the OpenSCAD file:

// Author: Tiago Charters de Azevedo
// Maintainer: Tiago Charters de Azevedo

// Copyright (c) - 2016 Tiago Charters de Azevedo (tca@diale.org)

// This program is free software; you can redistribute it and/or modify
// it under the terms of the GNU General Public License as published by
// the Free Software Foundation; either version 3, or (at your option)
// any later version.

// This program is distributed in the hope that it will be useful,
// but WITHOUT ANY WARRANTY; without even the implied warranty of
// MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
// GNU General Public License for more details.

// You should have received a copy of the GNU General Public License
// along with this program; if not, write to the Free Software
// Foundation, Inc., 51 Franklin Street, Fifth Floor,
// Boston, MA 02110-1301, USA.


// Gravity aceleration
g=9.8; //(m/s^2)
rhoair=0.001225; // (g/cm^3)
// pi
pi=3.1415926;

/*Drag coeficiente
.5 sphere
see: https://en.wikipedia.org/wiki/Drag_coefficient
*/
Cd=.47;

// Ping-Pong
D=.04; // (m)
mball=2.7; // (g)
A=pi*pow(D/2,2);
rhoball=mball/(4*pi/3*pow(100*D/2,3));// 0.081; // (g/cm^3)

// Font size
fsize=4;

R=100;
h=2;

coef=1;//3.6*0.621371;
module slice(h=2){
    difference(){
        cylinder(h,R,R,center=true,$fn=64);
        translate([0,2.5*R/2,0]){
            cube([2.5*R,2.5*R,2*h],center=true);}
        translate([2.5*R/2,0,0]){
            cube([2.5*R,2.5*R,2*h],center=true);}}}

module vscale(){
    for(alpha=[0:5:89]){
        v=coef*sqrt(pi*g*rhoball*pow(D,3)*tan(alpha)/(3*A*Cd*rhoair));
        rotate([0,0,alpha]){
            translate([-R*.99,0,-0]){
                rotate([0,0,-0]){
                    linear_extrude(height=h,scale=1,twist=0,convexity= 0){
                        text(str(floor(v*10)/10),size=fsize,font="Arial Black:style=Bold",center=true);}}}

            translate([-R*.8,-1*0,h/2]){
                sphere(h/2,center=true,$fn=64);}}}

    translate([-R*.7,-1*0,h/2]){
        sphere(h/2,center=true,$fn=64);}


    translate([0,-R+2,0]){
        rotate([0,0,90]){
            linear_extrude(height=h,scale=1,twist=0,convexity= 0){
                text("m/s",size=fsize,font="Arial Black:style=Bold",center=true);}}}}

//difference()
{
    intersection(){
        union(){
            difference(){
                slice();
                cylinder(10,R*.7,R*.7,center=true,$fn=64);}
            translate([0,-R/2,0]){
                cube([6*h,R,h],center=true);}
            translate([-R/2,0,0]){
                cube([R,6*h,h],center=true);}}
        cylinder(10*h,R,R,center=true,$fn=64);}
    vscale();}


cylinder(h,3*h,3*h,center=true,$fn=64);

difference(){
    union(){
        cylinder(3*h,h,h,center=false,$fn=64);
        translate([0,0,3*h]){
    sphere(h,center=true,$fn=64);}}
    translate([0,0,2.5*h]){
        rotate([0,90,0]){
            cylinder(3*h,1,1,center=true,$fn=64);}}}

---

For attribution, please cite this page as:

Charters, T., "Ping-Pong Anemometer": https://nexp.pt/Ping-Pong-Anemometer.html (19-12-2024 [09:00])

---

(cc-by-sa) Tiago Charters - tiagocharters@nexp.pt