Principle of least constraint

Equações de movimento e resolução numérica do movimento de um ponto material sobre uma superfície

Uma das imagens que sempre me cativou, a representação do movimento de um ponto material sobre uma superfície apenas sujeito ao seu próprio peso. Essa mesma figura é recorrente em muitos livros de física em particular em livros de gravitação, e em livros de divulgação, dita, científica. No entanto, apesar de todo o rigor inerente a qualquer um dos dois tipos de publicação, as equações usadas para construir essas figuras nunca aparecem.

Certamente por aquelas serem, é uma hipótese, uma representação de artista que tenta capturar a ideia rigorosa que se quer ilustrar.

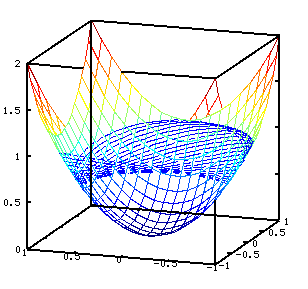
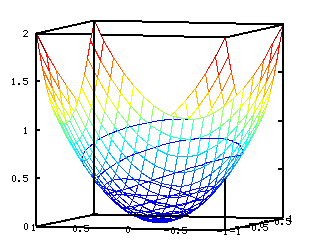
As duas figuras seguintes mostram o movimento de um ponto material sobre um parabolóide, a primeira sem atrito e a segunda com atrito, com as mesmas condições iniciais [0 1 1 0] (ver código em Octave mais à frente).

sem atrito (k=0)

com atrito (k=.05)

Vejamos então como construir as equações. Uma das formas de as obter é usando o Principle of least constraint, que pode se visto como um certo tipo de método dos mínimos quadrados. Tem o seguinte enunciado para um único ponto material: a aceleração de um ponto material minimiza a quantidade 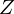$latex2png equation$ para quaisquer restrições cinemáticas

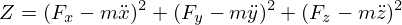
$latex2png equation$

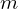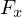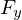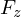onde $latex2png equation$ , $latex2png equation$ , $latex2png equation$ e $latex2png equation$ , são respectivamente a massa e as componentes da força a que está sujeito o ponto.

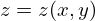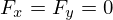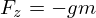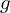Como queremos obter a trajectória de um ponto material que se move sobre um superfície apenas sujeito ao seu próprio peso, vem que, $latex2png equation$ e que $latex2png equation$ e $latex2png equation$ onde $latex2png equation$ é a aceleração da gravidade (uma constante positiva).

É condição necessária para a existência de um mínimo que

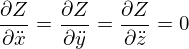
$latex2png equation$

e obtém-se

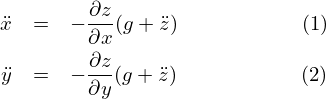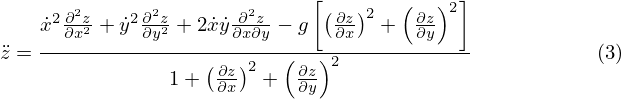
$latex2png equation$ onde $latex2png equation$

Esta última equação obtém-se de

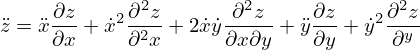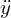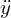$latex2png equation$ usando as equações de $latex2png equation$ e $latex2png equation$ .

O passo seguinte consiste em implementar a resolução numérica das equações (1) e (2) em Octave. Assim, o sistema de e.d.o's é implementado pela função em Octave f.m, para o caso de 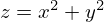$latex2png equation$

function xdot=f(x,t)
  dfdx=2*x(1);
  dfdy=2*x(3);
  d2fdx2=2;
  d2fdy2=2;
  d2fdxdy=0;
  g=1;
  k=0.05;
  xdot = zeros (4,1);
  d2z=(x(2)^2*d2fdx2+x(4)^2*d2fdy2+2*x(2)*x(4)*d2fdxdy-g*(dfdx^2+dfdy^2))/(1+dfdx^2+dfdy^2);
  xdot(1)=x(2);
  xdot(2)=-k*x(2)-dfdx*(g+d2z);
  xdot(3)=x(4);
  xdot(4)=-k*x(4)-dfdy*(g+d2z);
endfunction;

onde se inclui um termo de dissipação, proporcional ás velocidades, com coeficiente de atrito k. Os comandos para gerar os gráficos anteriores são

#1

clear all
clf

l=1;
xl=linspace(-l,l,20);
yl=linspace(-l,l,20);
[x y]=meshgrid(xl,yl);


t = linspace (0, 100, 1000);
xini=[0 1 1 0]
z = lsode ("f", xini, t);

hold on

mesh(x,y,x.^2+y.^2)
plot3(z(:,1), z(:,3),z(:,1).^2+ z(:,3).^2,'b')

As duas imagens seguintes mostram outras versões das mesmas figuras assim como os retratos de fase para cada uma da coordenadas

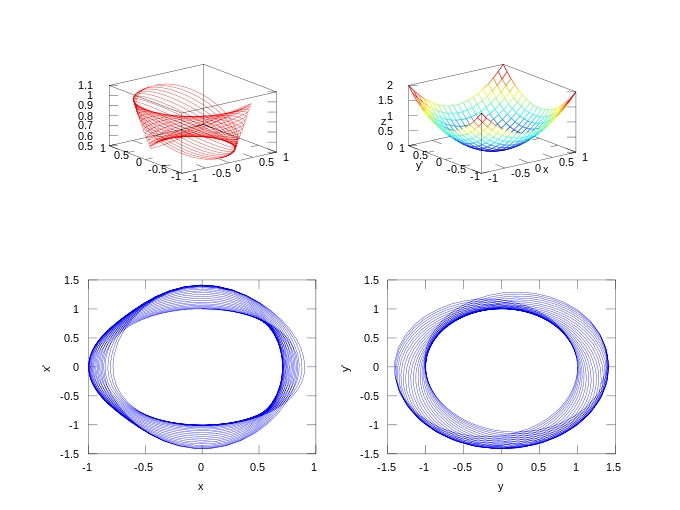sem atrito (k=0)

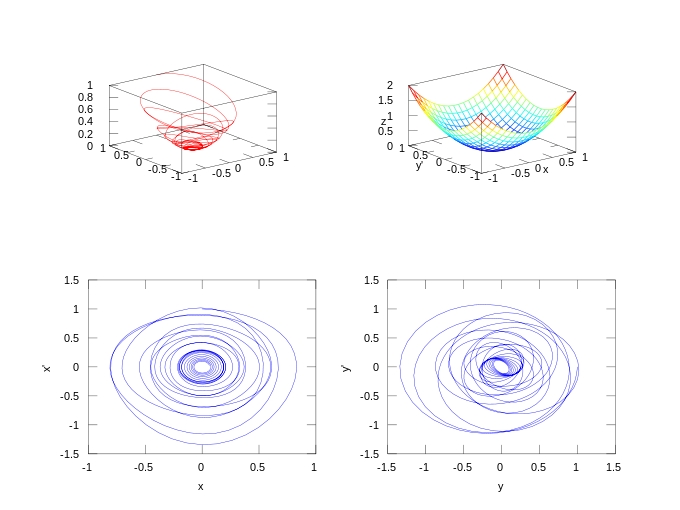com atrito (k=.05)

Palavras chave/keywords: matemática, física, Gauss, Principle of least constraint

Criado/Created: NaN

Última actualização/Last updated: 10-10-2022 [14:25]

Voltar à página inicial.