Aprops do COVID19
Bacillus dendroides e a equação logística
O modelo logístico assume que o crescimento inicial de uma população com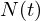 
indivíduos aumenta exponencialmente com taxa de crescimento constante e
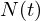à medida que aproxima-se do limite máximo
e a taxa de crescimento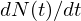 
diminui ando origem a uma curva tipo-S.
Os mecanismos que causam este abrandamento dependem da caracterização da população, ou do sistema a ser modelado, mas estudos empíricos mostram que este comportamento está presente em processos de crescimento e difusão, onde existe um sistema de feedback associado e.g. restrições ao uso de alimento, espaço físico, hospedeiros no caso de propagação viral, etc. Assim o modelo logístico é um modelo genérico que modela sistemas com mecanismos conhecidos mas também com propriedades escondidas.
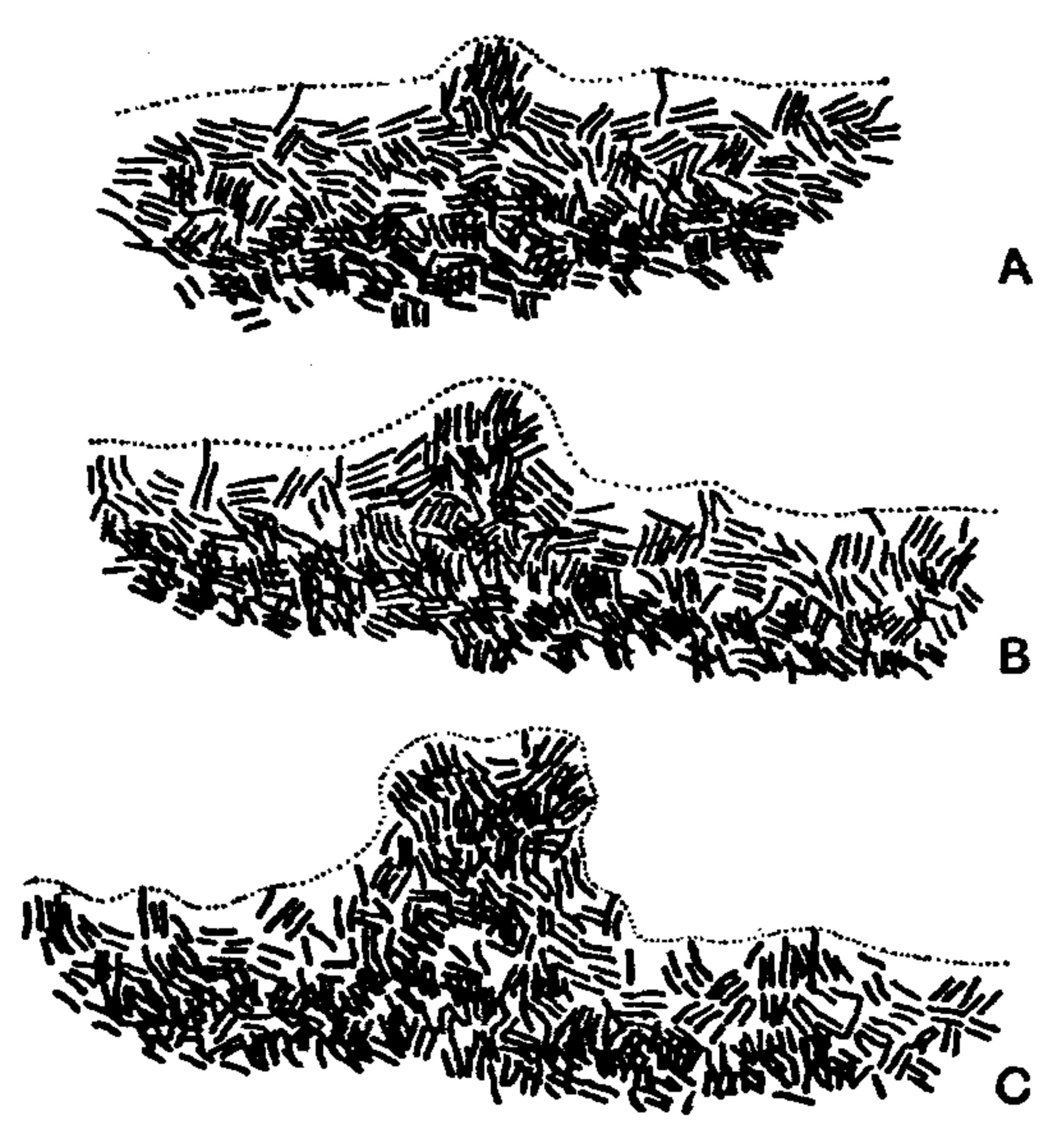
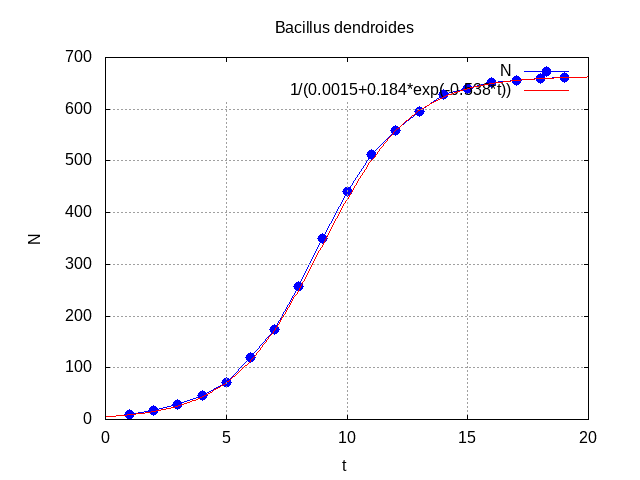
O caso clássico é do crescimento da bactéria Bacillus dendroides1.
A figura seguinte mostra os sucessivos estágios de desenvolvimento da bactéria
Bacillus dendroides num período de 6 horas numa solução de
agar-agar. Neste caso usa-se a área ocupada pelo crescimento como
medida do número de B. dendroides em instantes sucessivos (
).
É possível modelar o crescimento de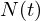
indivíduos de uma determinada população através de uma equação
diferencial, equação logística, com a forma
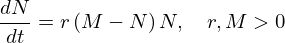
A solução da equação anterior com condição inicial
(
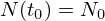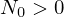) é dada por
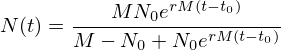
O valor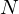 
atinge metade do valor máximo
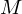no instante
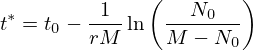
Outra forma de escrever a solução da equação e que é mais útil para estimar os parâmetros relevantes é3:
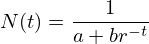
1. R. Pearl, ‘‘The Growth of Population’’ Quart. Rev. Biol. 2, 532–548, (1927)
2. H. G. Thornton, On the development of a standardized agar medium for counting soil bacteria Ann. Appl. Biol., 9:241-274, (1922)
3. C. Mar-Molinero, Tractors in Spain: A Logistic Analysis, The Journal of the Operational Research Society, Vol. 31, No. 2, pp. 141-152 (1980)
Palavras chave/keywords:Criado/Created: 11-03-2020 [16:56]
Última actualização/Last updated: 10-10-2022 [14:25]
(c) Tiago Charters de Azevedo