Algoritmo de Horner para polinómios

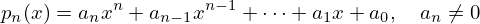As funções mais simples em matemática são os polinómios. Um polinómio é uma função com a forma $latex2png equation$ Como é fácil de ver para calcular o valor do polinómio num ponto é apenas necessário fazer umas quantas multiplicações e somas. A maneira mais eficiente de calcular o valor do polinómio num ponto, isto é, efectuando o menor número de produtos e somas, é conseguido através do algoritmo de Horner. 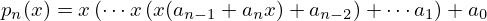Consiste em factorizar o polinómio na seguinte forma: $latex2png equation$

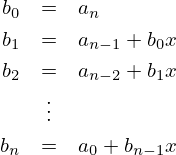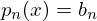
A maneira mais simples de pensar numa implementação computacional é considerar a sucessão $latex2png equation$ onde o resultado final é $latex2png equation$

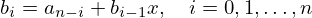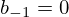
Mais geralmente pode por-se $latex2png equation$ com $latex2png equation$

Apesar da sua forma simples e definida por recurrência a sucessão de valores é mais clara e simples quando construída de uma forma imperativa do que a sua versão funcional. Se não veja-se. A implementação funcional fica:

(defun horner-eval (x coef)
  (accumulate (lambda (a b)
                (+ a (* b x)))
              0
              coef))

(defun accumulate (op initial sequence)
  (if (not sequence)
      initial
      (funcall op (car sequence)
          (accumulate op initial (cdr sequence)))))

enquanto a versão imperativa do mesmo algoritmo tem a forma:

(defun polyval (x coef)
  (let ((coefx coef) (px 0))
    (while coefx
      (setq px (+ (* x px)  (car coefx)))
      (setq coefx (cdr coefx)))
    px))

Created: NaN

Last updated: 23-01-2025 [00:04]

For attribution, please cite this page as:

Charters, T., "Algoritmo de Horner para polinómios": https://nexp.pt/horner.html (23-01-2025 [00:04])

(cc-by-sa) Tiago Charters - tiagocharters@nexp.pt