Tiago Charters work gallery about contact

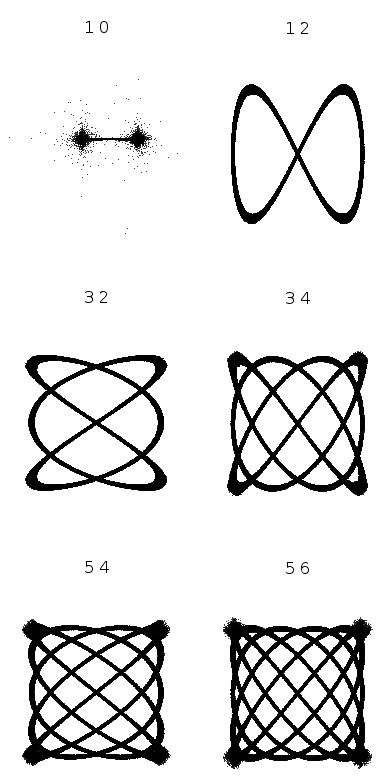
6 figuras de Lissajous.

A imagem anterior mostra 6 figuras de Lissajous com equações 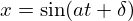, 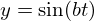para diferentes valores de a e b com delta nulo. A ideia foi desenha-las como se fossem construídas deixando cair tinta de uma lata a fluxo constante. Assim a grossura do traço depende da velocidade a que a curva é percorrida em cada instante de modo a que a área coberta pela tinta por unidade de tempo seja constante. O código em Octave é constituído de duas partes: uma caneta

function retval=pen(x,r,n)
  theta=rand(1,n);
  retval=[r*rand(1,n).*cos(2*pi*theta)+x(1); r*rand(1,n).*sin(2*pi*theta)+x(2)];
endfunction;

e o código para desenhar cada uma das figuras (basta ler o que lá está)

clf;
clear all
n=2000;
theta=linspace(0,1,n);
delta=0;
k=1;
for i=1:2:5
  a=i;
  for j=i-1:2:i+1
    [i j k]
    b=j;
    u=sin(2*pi*a*theta+delta);
    v=sin(2*pi*b*theta);
    du=diff(u);
    dv=diff(v);
    damp=du.^2+dv.^2;
    damp=damp/max(damp);
    amp=.025;
    r=amp./(0+sqrt(damp));
    subplot(3,2,k)

    plot(u,v,'k')
    hold on

    for l=1:n-1
      x=pen([u(l) v(l)],r(l),floor(10/r(l)));
      plot(x(1,:),x(2,:),'k.')
    endfor;
    title(sprintf('%i %i',[i j]))
    axis off square
    k=k+1;
  endfor;
endfor;

---

For attribution, please cite this page as:

Charters, T., "Figuras de Lissajous": https://nexp.pt/lissajous.html (23-01-2025 [00:04])

---

(cc-by-sa) Tiago Charters - tiagocharters@nexp.pt