Métodos numéricos em GNU/Octave

Breve curso de métodos numéricos em GNU/Octave: uma introdução computacional.

É dada permissão para copiar, distribuir e/ou modificar todos os programas/textos aqui disponibilizados nos termos da GNU GENERAL PUBLIC LICENSE Versão 3 ou qualquer outra versão posterior publicada pela Free Software Foundation. Uma cópia da licença - GNU GENERAL PUBLIC LICENSE.

Nota prévia: Os métodos seguintes implementados foram pensados para uso demonstrativo, por isso, para os correr é necessário formatar o output usando o comando format short g. De modo a não permitir que o Octave quebre as linhas é necessária a instrução split_long_rows=0.

Equações não lineares

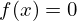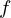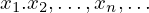Os métodos que aqui se disponibilizam permitem resolver equações do tipo $latex2png equation$ , onde $latex2png equation$ é uma função real de variável real não linear. Na maioria dos métodos é necessário fornecer uma aproximação inicial $latex2png equation$ ao zero da função sendo depois gerado uma secessão de aproximações $latex2png equation$ , que convergem para a solução da equação.

Método da bissecção

O método da bissecção, também chamado de método de divisão binária, é um dos métodos básicos para o cálculo numérico de zeros de funções. É baseado no teorema de Bolzano, e logo, a convergência do método só pode ser garantida se a função 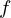$latex2png equation$ , cujo zero se quer determinar, for uma função contínua.

A função $latex2png equation$ é definida por

function fv = f (x)
  fv=e^x+2^(-x)+2*cos(x)-6;
endfunction

O código em Octave que implementa o método é este:

function bissec(a,b,Niter,tol)
  disp("")
  disp ("Output for the Bisection method")
  disp("")
  disp ("           n           a           b           x         f(x)")
  fa=f(a);
  for i=1:Niter
    fb=f(b);
    x=(b+a)/2;
    fx=f(x);

    disp ([i, a, b, x, fx]);
    if (fx==0 |(b-a)/2<tol)
      disp("")
      disp ("The method completed successfully!")
      disp("")
      return;
    else
      if (fa*fx>0)
        a=x;
        fa=fx;
      else
        b=x;
      endif
    endif
  endfor
  disp("")
  disp ("The method failed after (Niter)")
  disp (Niter)
  disp ("iterations")
  disp("")
endfunction

Método do ponto fixo

function fpoint(x,Niter,tol)
  disp("")
  disp ("Output for the Fixed Point method")
  disp("")
  disp ("           n          x          err        g(x)")
  for i=1:Niter
    oldx=x;
    x=g(x);
    if (g(x)==x |abs(x-oldx)<tol)
      disp("")
      disp ("The method completed successfully!")
      disp("")
      return;
    else
      epsilon=abs(x-oldx);
      disp ([i-1,oldx, epsilon, g(x)]);
    endif
  endfor
  disp("")
  disp ("The method failed after (Niter)")
  disp (Niter)
  disp ("iterations")
  disp("")
endfunction

Método de Newton

function fv = f (x)
  fv=e^x+2^(-x)+2*cos(x)-6;
endfunction

function dfv = df (x)
  dfv= e^x-2^(-x)*log(2)-2*sin(x);
endfunction

function newton(xo,Niter,tol)
  disp("")
  disp ("Output for the Newton method")
  disp("")
  disp ("           n          x          err        f(x)")
  for i=1:Niter
    x=xo-f(xo)/df(xo);
    if (f(xo)==0 |abs(x-xo)<tol)
      disp("")
      disp ("The method completed successfully!")
      disp("")
      return;
    else
      epsilon=abs(x-xo);
      disp ([i-1, xo, epsilon, f(xo)]);
      xo=x;
    endif
  endfor
  disp("")
  disp ("The method failed after (Niter)")
  disp (Niter)
  disp ("iterations")
  disp("")
endfunction

Método da secante

function secant(x,y,Niter,tol)
  disp("")
  disp ("Output for the Secant method")
  disp("")
  disp ("           n           x         err        f(x)")

  for i=1:Niter
    if (f(x)==0 |abs(x-y)<tol)
      disp("")
      disp ("The method completed successfully!")
      disp("")
      return;
    else
      epsilon=abs(x-y);
      disp ([i-1,x, epsilon, f(x)]);
      oldx=y;
      y=y-f(y)*(y-x)/(f(y)-f(x));
      x=oldx;
    endif
  endfor
  disp("")
  disp ("The method failed after (Niter)")
  disp (Niter)
  disp ("iterations")
  disp("")
endfunction

Método falsa posição (regula falsi)

function regulafalsi(x,y,Niter,tol)
  disp("")
  disp ("Output for the Regula Falsi method")
  disp("")
  disp ("           n           a           b          x         f(x)")
  for i=1:Niter
    oldy=y;
    y=y-f(y)*(y-x)/(f(y)-f(x));
    if (f(y)==0 |abs(y-x)<tol)
      disp("")
      disp ("The method completed successfully!")
      disp("")
      return;
    else
      epsilon=abs(oldy-x);
      disp ([i,x, oldy, y, f(y)]);
      if (f(x)*f(y)<0)
      else
        x=y;
        y=oldy;
      endif
    endif
  endfor
  disp("")
  disp ("The method failed after (Niter)")
  disp (Niter)
  disp ("iterations")
  disp("")
endfunction

Método de Newton para sistemas de equações não lineares

function Fv=Ffun(x)
  Fv(1,1)=x(1).*x(2)+x(2).^2-2;
  Fv(2,1)=x(1).^2-x(1).*x(2);
endfunction

function Jv=Jfun(x)
  Jv(1,1)=x(2);
  Jv(1,2)=x(1)+2*x(2);
  Jv(2,1)=2*x(1)-x(2);
  Jv(2,2)=-x(1);
endfunction

function [x Fv]=newtonsys(xo,Niter,tol)

  x=xo';
  for i=1:Niter

    delta=eye(length(xo),1);
    if (Ffun(x)== zeros(length(xo),1) | abs(max(delta))<=tol)
      disp("")
      disp ("The method completed successfully!")
      disp (Niter)
      disp("")
      return;
    else
      Jv=Jfun(x);
      Fv=Ffun(x);
      delta=-Jv\Fv;
      x=x+delta;
    endif
  endfor
  disp("")
  disp ("The method failed after (Niter)")
  disp (Niter)
  disp ("iterations")
  disp("")

endfunction

Sistemas de equações lineares

Métodos directos — Condensação de Gauss

function x=gaussel(A,b)
  n=length(b);
  for k=1:n-1
    for i=k+1:n
      m=A(i,k)/A(k,k);
      for j=k:n
        A(i,j)=A(i,j)-m*A(k,j);
      endfor
      b(i)=b(i)-m*b(k);
    endfor
  endfor

  x(n)=b(n)/A(n,n);
  for i=n-1:-1:1
    sum=b(i);
    for j=i+1:n
      sum=sum-A(i,j)*x(j);
    endfor
    x(i)= sum/A(i,i);
  endfor
endfunction

function [A b x]=gausselk(A,b)
  n=length(b);
  augm=[A b]
  for k=1:n-1
    for i=k+1:n
      m=A(i,k)/A(k,k)
      for j=k:n
        A(i,j)=A(i,j)-m*A(k,j);
      endfor
      b(i)=b(i)-m*b(k);
    augm=[A b]
    endfor
  endfor

x=inv(A)*b;

endfunction

Métodos iterativos

Método de Jacobi

function xout=jacobi(A,b,Niter,tol)
  n=length(A);
  D=diag(diag(A));
  L=D-tril(A);
  U=D-triu(A);
  invD=diag(1./diag(A));
  x=zeros(n,1);
  xout=x;
  oldx=ones(n,1);
  for i=1:Niter
    if (max(abs(x-oldx))<tol)
      disp("")
      disp ("The method completed successfully!")
      disp("Niter")
      disp(i)
      disp("")
      return;
    else
      oldx=x;
      x=(invD*(L+U))*x+invD*b;
      xout=[xout x];
    endif
  endfor
  disp ("Maximum number of iterations exceeded!")
endfunction

Método de Gauss-Seidel

function xout=gaussseidel(A,b,Niter,tol)
  n=length(A);
  D=diag(diag(A));
  L=D-tril(A);
  U=D-triu(A);
  invDL=inv(D-L);
  x=zeros(n,1);
  xout=x;
  oldx=ones(n,1);
  for i=1:Niter
    if (max(abs(x-oldx))<tol)
      disp("")
      disp ("The method completed successfully!")
      disp("Niter")
      disp(i)
      disp("")
      return;
    else
      oldx=x;
      x=invDL*U*x+invDL*b;
      xout=[xout x];
    endif
  endfor
  disp ("Maximum number of iterations exceeded!")
endfunction

Interpolação polinomial

Polinómio interpolador de Newton — diferenças divididas

function dd=newtondd(x,y)
  disp("")
  disp ("Output for the divided diferences")
  disp("")
  for i=1:length(x)
    dd(i,1)=y(i);
  endfor
  for i=2:length(x)
    for j=2:i
      dd(i,j)=(dd(i,j-1)-dd(i-1,j-1))/(x(i)-x(i-j+1));
    endfor
  endfor
  dd=[x' dd];
endfunction

Método dos mínimos quadrados

Caso discreto

function [a b c]=lsquare(x,y,n)
  for i=1:n+1
    for j=1:n+1
      a(i,j)=sum(x.^(j+i-2));
    endfor
  endfor
  for i=1:n+1
    b(i)=sum(y.*x.^(i-1));
  endfor
  b=b';
  c=a\b;
  lsquarev=[a b c];
endfunction

Integração numérica

Regras dos Trapézios

function inttrap(a,b,n)
   h=(b-a)/n;
   x=[a:h:b];
   I=h/2.*(2*sum(f(x))-f(a)-f(b));
endfunction

Regra de Simpson

function I=intsimpson(a,b,n)
   k=[0:n];
   h=(b-a)/(n);
   x=[a:h:b];
   aux1=sum(mod(k,2).*f(x));
   aux2=sum((1-mod(k,2)).*f(x));
   I=h/3.*(2*aux2+4*aux1-f(a)-f(b));
endfunction

Interpolação fractal

function [px py]=interpfrac(x,y,d,npoints)
  n=length(x);
  b=x(n)-x(1);

  for i=2:n
    aw(i-1)=(x(i)-x(i-1))/b;
    ew(i-1)=(x(n)*x(i-1)-x(1)*x(i))/b;
    cw(i-1)=(y(i)-y(i-1)-d(i)*(y(n)-y(1)))/b;
    fw(i-1)=(x(n)*y(i-1)-x(1)*y(i)-d(i)*(x(n)*y(1)-x(1)*y(n)))/b;
  endfor

  oldx=0;
  oldy=0;
  px=oldx;
  py=oldy;
  for j=1:npoints
    k=floor((n-1)*rand)+1;
    newx=aw(k)*oldx+ew(k);
    newy=cw(k)*oldx+d(k)*oldy+fw(k);
    oldx=newx;
    oldy=newy;
    px=[px; newx];
    py=[py; newy];
  endfor
endfunction

Palavras chave/keywords: métodos numéricos, GNU/Octave

Criado/Created: NaN

Última actualização/Last updated: 04-10-2021 [18:00]

Voltar à página inicial.