Rt: previsões para que te quero
Os dados que nos chegam todos os dias reportados pela DGS não nos dão o verdadeiro estado de evolução de epidemia. Precisamos de dados mais robustos para que se possa avaliar a evolução do coronavirus em tempo real.
Há uma grandeza, um número, que nos diz a "taxa" à qual o vírus se transmite, R-zero (R0), o número básico de reprodução. Diz-nos qual o número de pessoas, em média, que uma pessoa infetada contaminará numa comunidade onde não existe imunidade. O valor de R0 pode variar de país para país, de região para região, devido a flutuações na distribuição de idades ou diferenças culturais de interação social.
A versão efetiva deste número, Rt, o número de reprodução num determinado dia t, é o valor atualizado da taxa de transmissão num dado momento. Varia consoante as medidas de controlo da epidemia, isolamento físico, quarentena, restrições de viagens e mobilidade, encerramento de escolas, uso de máscaras, etc, ...
Por isso é fácil perceber o quanto é necessário e relevante ter dados robustos, abertos, peer-reviewd e com metodologias bem estabelecidas, para que possamos tomar decisões racionalmente informadas. Devemos ser críticos relativamente aquilo que comentadores, órgãos de comunicação social e redes sociais nos alimentam todos os dias.
Há junk food também há junk information.
Precisamos assim de saber em cada dia qual é a real capacidade do vírus em se propagar e consequentemente perceber este número de reprodução efetivo Rt em cada contexto particular, seja de um país, região ou cidade.
Não só o levantamento das restrições a que voluntariamente nos temos submetido depende do conhecimento deste número como também a imposição de mais restrições depende dele. Precisamos de saber.
Se o valor deste número de reprodução efetivo depende das condições locais e culturais onde o vírus se propaga então segue que não há uma solução que dê para todos, o que funciona, digamos, na Suécia, não funcionará em Portugal através de um simples copy&paste. É fácil construir argumentos do tipo: "preferiria proteger a economia e assumir os riscos com a epidemia", "já estou a dar em doido não aguento mais 3 meses", "não vale a penas nos preocuparmos com a economia que ela recupera depois, depois de isto tudo passar e sobrevivermos como comunidade". O espectro de argumentos é grande mas não devemos deixar de formar e participar nesta discussão.
No entanto, em qualquer um dos cenários preferidos, há uma propriedade comum. O regresso à vida normalizada será concretizada por ciclos de abertura-fechamento1 até que se atinja a imunidade de grupo ou se descubra uma vacina.
Para isso precisamos de fazer umas contas e de saber como estimar Rt em cada dia. A figura seguinte mostra o número de reprodução efetivo para Portugal. Há várias maneiras/algoritmos de o calcular. O utilizado para a estimativa da figura foi o trabalho de Luís Bettencourt, Ruy Ribeiro2 que tive conhecimento no maravilhoso texto3 e código em Python de Kevin Systrom.
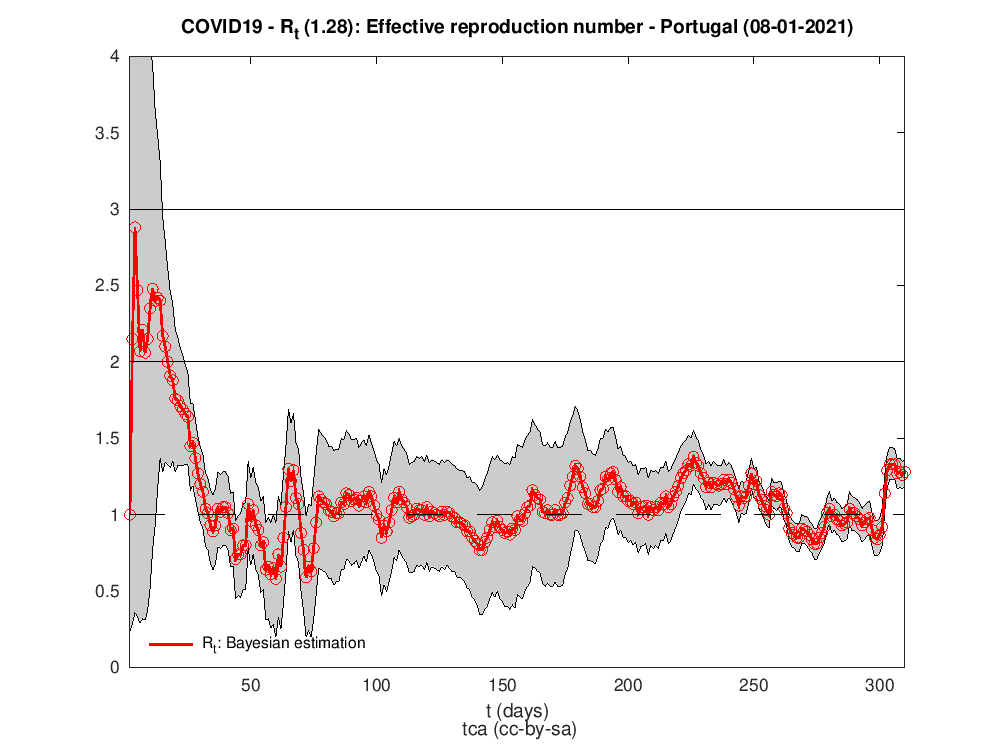
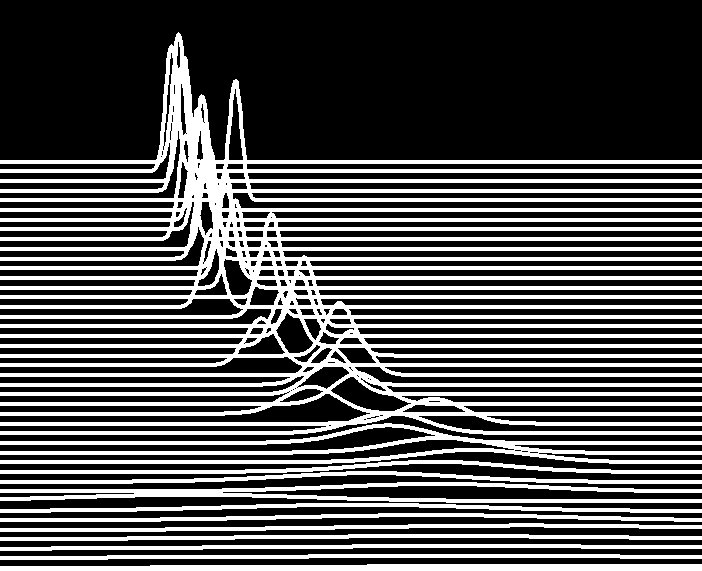
Não vou repetir as explicações técnicas do Systrom mas deixo aqui as sucessivas distribuições de Poisson usadas no cálculo Bayesiano das estimativas de Rt. Dava uma capa bem gira para um álbum de música ;) ou t-shirt.
Gráficos de Rt para vários países: https://www.nexp.pt/covid19RtWorld/
Dados: https://opendata.ecdc.europa.eu/covid19/casedistribution/csv
Rt para as diferentes regiões do país
Os dados para Portugal são da DAta science for social good PT - dssgpt: https://github.com/dssg-pt/covid19pt-data

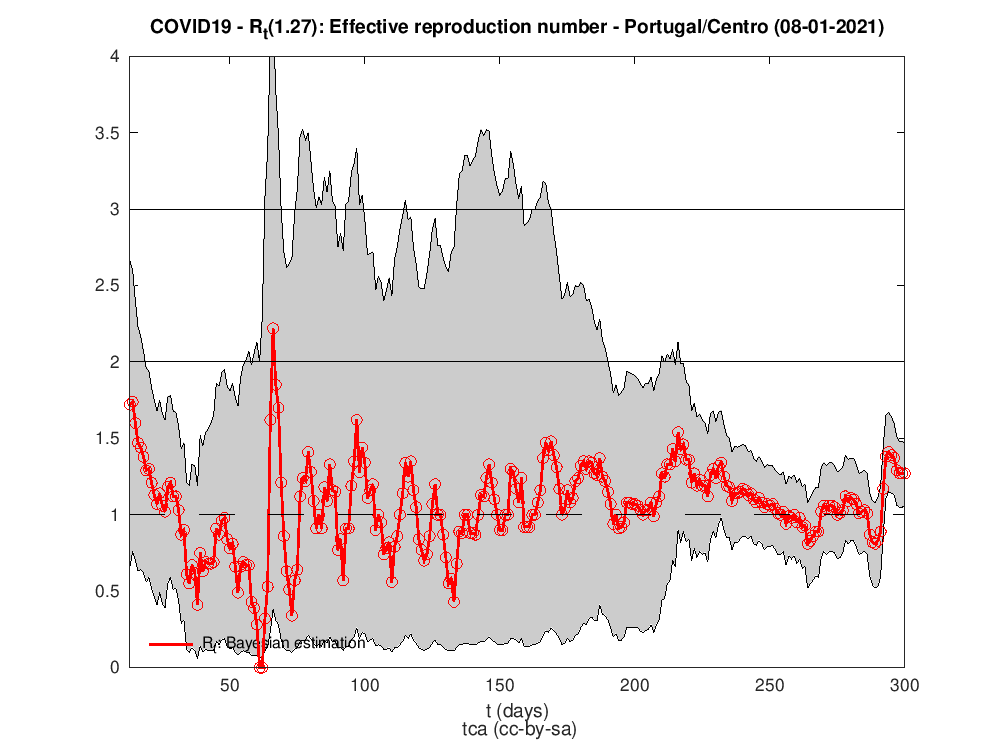
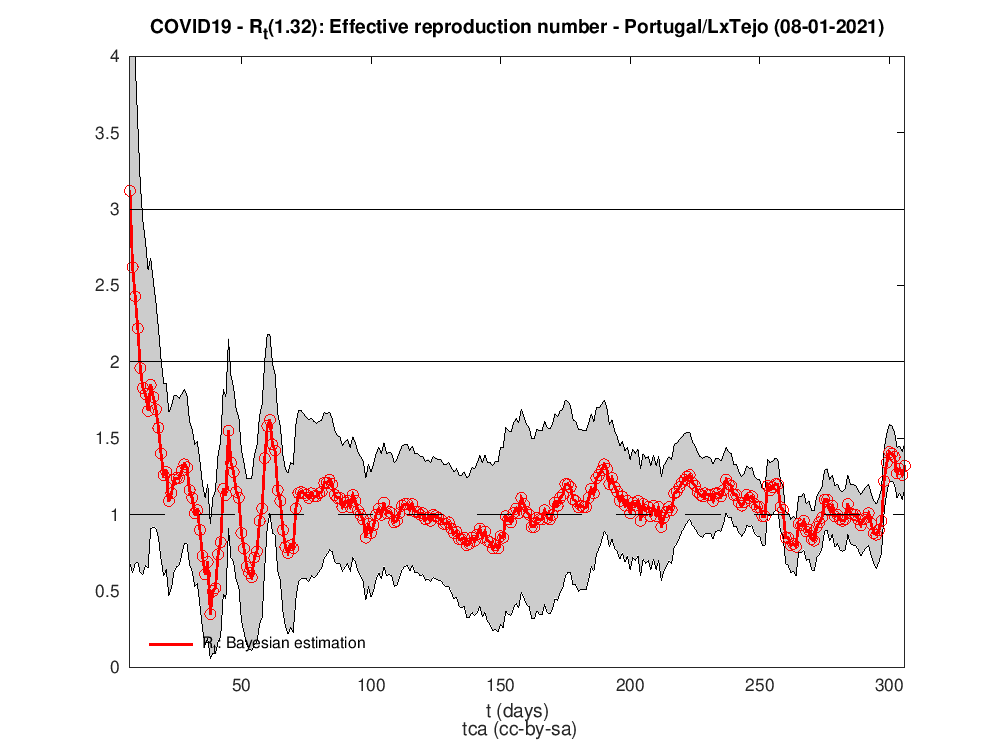
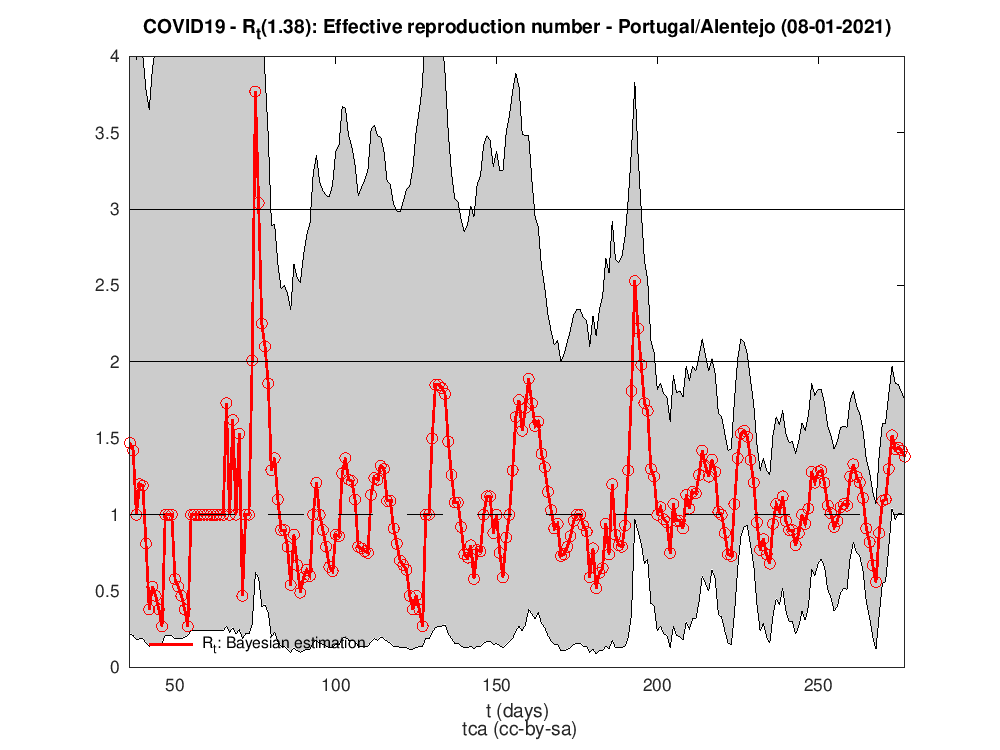
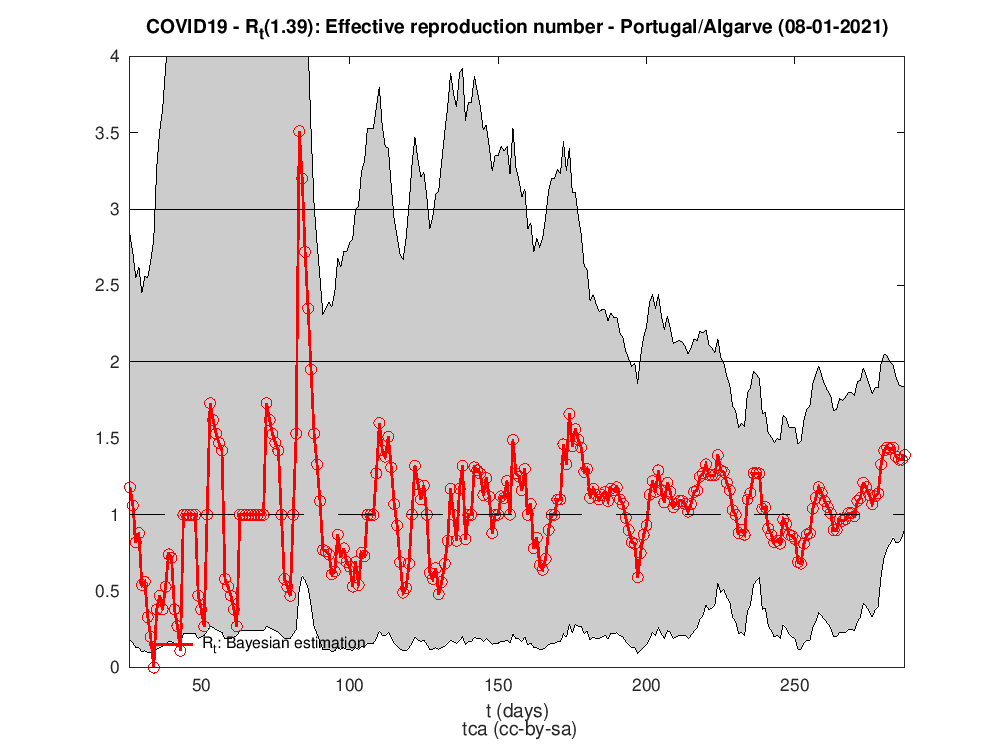
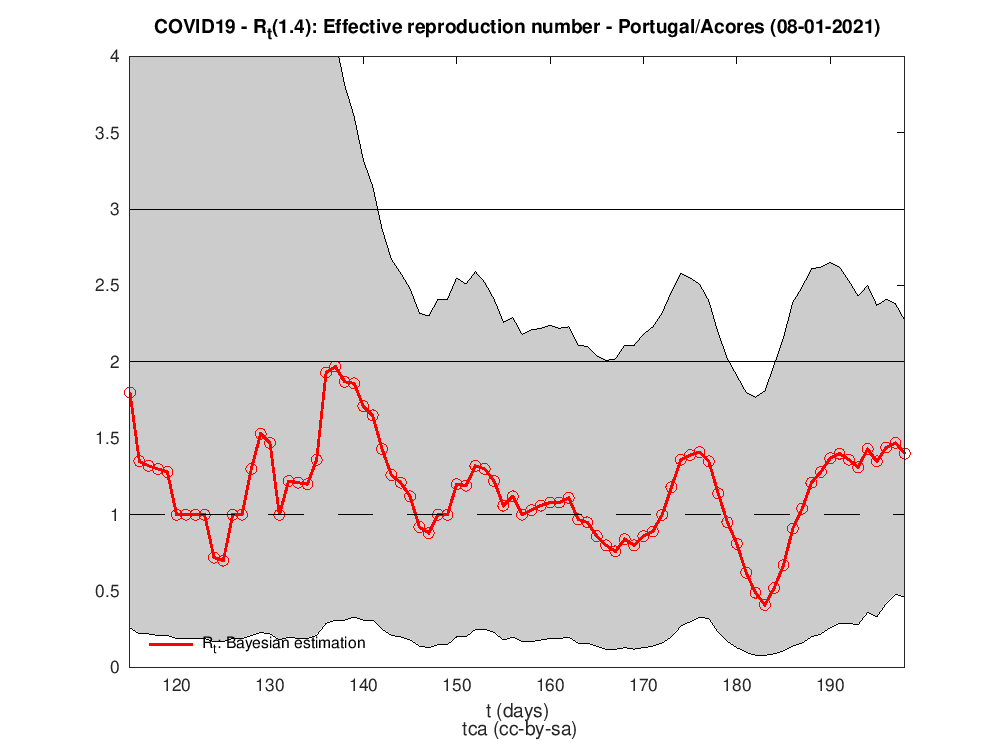
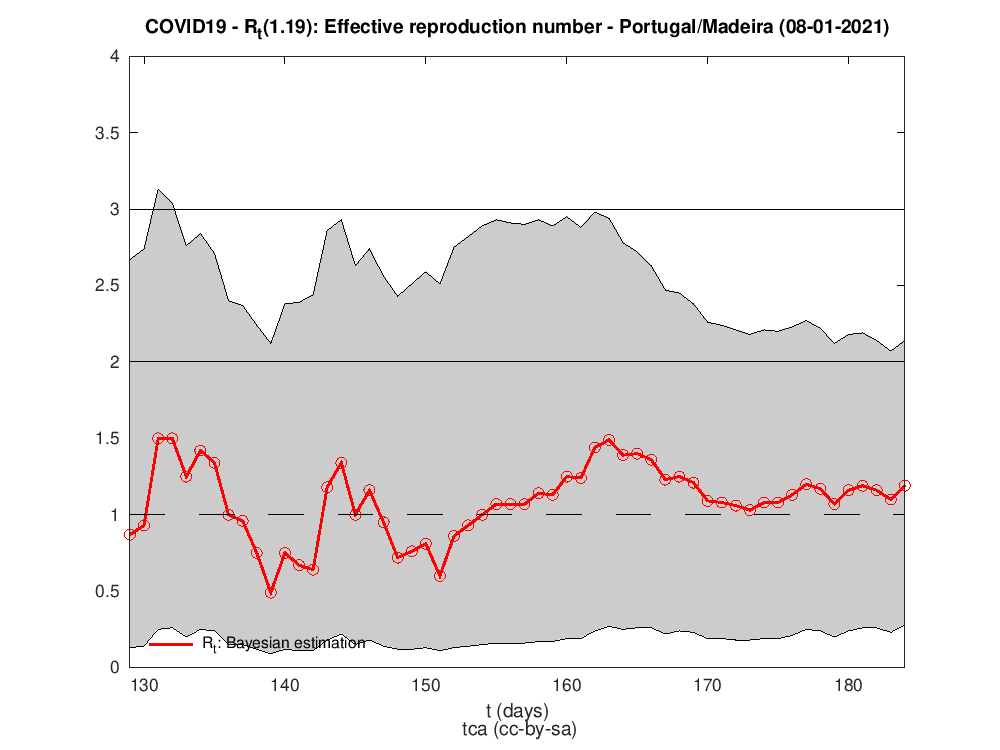
P.S. A regra dos trapézias faz das suas no cálculo do HDI.
Duas notas
Deixo também o código em GNU/Octave para futuros divertimentos. Claro que existem soluções enlatadas que permitiriam calcular o Rt sem esforço e.g. o software de estatística R tem uma biblioteca que faz isso mesmo.
Mas qual é a graça de fazer isso. ;)
“Neo, sooner or later you’re going to realize, just as I did, that there’s a difference between knowing the path and walking the path.” - Morpheus
Outra nota (21/04/2020): O texto que estava aqui inicialmente incluía um código em GNU/Octave. Infelizmente tinha um gato ;) Colocarei o código correto nos próximos dias.
Foi só hoje de manhã, enquanto lavava os dentes, que descobri o "erro". Uma coisa coisa estúpida que têm todos os erros depois de descobertos. Fui buscar os valores para estimação ao CSV dos dados na coluna errada. Coisa positiva disto tudo: revirei o código todo do avesso. Até fui olhar para o código da distribuição de Poisson do Octave e que é opensource. Agradeço aos céticos o Twitter que insistentemente me recordavam que o cálculo estaria errado. Tinham razão! Obrigado.
Referências
1. Lockdown Can’t Last Forever. Here’s How to Lift It. April 6, (2020)
2. Luís M. A. Bettencourt, Ruy M. Ribeiro, Real Time Bayesian Estimation of the Epidemic Potential of Emerging Infectious Diseases (2008)
3. Estimating COVID-19's $R_t$ in Real-Time (2020)
Código em GNU/Octave
# Author: Tiago Charters de Azevedo ## Maintainer: Tiago Charters de Azevedo ## URL: https://nexp.pt ## Version: * ## Copyright (c) - 2020 Tiago Charters de Azevedo ## This program is free software; you can redistribute it and/or modify ## it under the terms of the GNU General Public License as published by ## the Free Software Foundation; either version 3, or (at your option) ## any later version. ## This program is distributed in the hope that it will be useful, ## but WITHOUT ANY WARRANTY; without even the implied warranty of ## MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the ## GNU General Public License for more details. ## You should have received a copy of the GNU General Public License ## along with this program; if not, write to the Free Software ## Foundation, Inc., 51 Franklin Street, Fifth Floor, ## Boston, MA 02110-1301, USA. ## Commentary: ## Python implentation: https://github.com/k-sys/covid-19/blob/master/Realtime%20R0.ipynb ## Paper: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0002185#pone.0002185.s001 ## Ref.: https://wwwnc.cdc.gov/eid/article/26/6/20-0357_article ## PT Data: https://raw.githubusercontent.com/dssg-pt/covid19pt-data/master/data.csv") clear all ## Clear it! ## load packages pkg load statistics pkg load signal ## Get the data from dssg-pt ## system("mv data.csv dataOLD.csv") ## system("wget https://raw.githubusercontent.com/dssg-pt/covid19pt-data/master/data.csv") ## Import all data x=importdata("data.csv"); n=diff(extractdata(x,"confirmados")); ## Testing with NY data ## https://github.com/k-sys/covid-19/blob/master/Realtime%20R0.ipynb ## nydata ## n=ny; ## n(n==0)=[]; date=extractdata(x,"data"); N=length(n); today=date{length(date)}; ############################################################ ## gamma (serial value) ## https://wwwnc.cdc.gov/eid/article/26/6/20-0357_article ## https://www.nejm.org/doi/full/10.1056/NEJMoa2001316 ############################################################ gamma=1/7; ############################################################ k=6; ## moving average window size (in days) (incubation day=5) dayinit=k+3; ## check plots ############################################################ ##Rtmavg=mavgrt(n,k,gamma); ##Rtmavg=[4.5 Rtmavg]; ############################################################ ## Use this for no filtering ##[Rt Rtm RtM]=bayesianrt(diff(n),gamma); ## Use this with k days moving average [Rt Rtm RtM]=bayesianrt(floor(filter(ones(1,k),k,n)),gamma); RtPT=Rt; ############################################################ ## Make plots ############################################################ figure(1) clf hold on ## Ploting HDI region area([dayinit:N],RtM([dayinit:N]),"FaceColor", [.8,.8,.8]); area([dayinit:N],Rtm([dayinit:N]),"FaceColor","w") ## Poting Bayesian estimation plot([dayinit:N],Rt([dayinit:N]),"linewidth",2,"ro") plot([dayinit:N],Rt([dayinit:N]),"linewidth",4,'r-;R_t: Bayesian estimation;') ## Plot mavg ##plot(Rtmavg,"linewidth",4,strcat("b-;R_t: geometric estimation mavg. (",num2str(k)," days);")) ## Plot some horizontal lines for legibility plot([0 100],[1 1],"linewidth",2,'k--') for i=2:4 plot([0 100],[i i],"linewidth",1,"k- -") end xlabel("t (days)") title(strcat("COVID19 - R_t (", num2str(floor(100*Rt(N))/100), "): Running basic reproduction number - Portugal (", date{length(date)}, ")")) box axis([dayinit N 0 5]) legend ("location", "SouthWest"); ## Write to file filename= strcat("00-Portugal-Rt-",today,"-COVID19PT.png"); print(filename,"-dpng") ############################################################ ############################################################ dayinit=16; reglist={"confirmados_arsnorte", "confirmados_arscentro", "confirmados_arslvt", "confirmados_arsalentejo", "confirmados_arsalgarve", "confirmados_acores", "confirmados_madeira"}; reglistaux={"Norte", "Centro", "LxTejo", "Alentejo", "Algarve", "Acores", "Madeira"}; for i=1:length(reglist) reglistaux{i} naux=extractdata(x,reglist{i}); naux(naux==0)=[]; nreg=diff(naux); N=length(nreg); # Rt1=mavgrt(nreg,k,gamma); # Rt1=[4.5 Rt1]; [Rt Rtm RtM]=bayesianrt(floor(filter(ones(1,k),k,nreg)),gamma); figure(i+1) clf hold on ## plot(nreg,"linewidth",4,strcat(colorl{i},'-;',reglistaux{i},";")) ## Ploting HDI region area(RtM,"FaceColor", [.8,.8,.8]); area(Rtm,"FaceColor","w") ## Ploting Bayesian estimation plot([dayinit:N],Rt([dayinit:N]),"linewidth",2,"ro") plot(Rt,"linewidth",4,'r-;R_t: Bayesian estimation;') plot([0 100],[1 1],"linewidth",2,'k--') ## Plot mavg ## plot(Rt1,"linewidth",4,strcat("b-;R_t: geometric estimation mavg. (",num2str(k)," days);")) ## Plot some horizontal lines for legibility plot([0 100],[1 1],"linewidth",2,'k--') for j=2:4 plot([0 100],[j j],"linewidth",1,"k- -") end xlabel("t (days)\n tca (cc-by-sa)") title(strcat(strcat("COVID19 - R_t(", num2str(floor(100*Rt(N-1))/100), "): Running basic reproduction number - Portugal/", reglistaux{i}, " (", date{length(date)}, ")"))) box axis([dayinit N 0 5]) legend ("location", "SouthWest"); ## Write to file filename= strcat("0",num2str(i),"-Portugal-Rt-",reglistaux{i},"-",today,"-COVID19PT.png"); print(filename,"-dpng") end system("montage *-Portugal* -geometry +1+1 -shadow Rt-montage-COVID19.png")
function retval=extractdata(x,field) m=5; ## data offset N=length(x); for i=1:N if (strcmp(strsplit(x{1},","){i},field)) k=i; break end end if (k==1) retval={}; for i=1:N-1-m retval{i}=strsplit(x{i+1+m},","){k}; end else retval=[]; j=1; for i=1:N-1-m aux=str2num(strsplit(x{i+1+m},","){k}); if (isnumeric(aux)) retval(j)=aux; j=j+1; end end end end
function [Rt Rtm RtM]=bayesianrt(n,gamma) ## https://github.com/k-sys/covid-19/blob/c26b5a1a432458f9039d3dca185f7ea1ed3d5c2d/Realtime%20R0.ipynb N=length(n); ############################################################ ############################################################ ## Do the Bayesian! ## Corona will tear us apart again. ############################################################ ############################################################ ## initialization RtMax=6; #max admissible value for Rt NRx=RtMax*100+1; Rx=linspace(0,RtMax,NRx); P1=ones(1,NRx); Rt(1)=4; ##Rt init value Pmatrix=[]; Rtm(1)=0; RtM(2)=RtMax; ############################################################ for i=2:N Pmatrix=[Pmatrix; P1]; P2=poisspdf(n(i),n(i-1)*exp(gamma*(Rx-1))); P1=P2/(trapz(Rx,P2)); ## normalization endfor Pmatrix=[Pmatrix; P1]; ## Check it out! ;) ## Plot Pmatrix distributions ## figure(10) ## clf; ## plot(Rx,[1:N]'+Pmatrix(1:N,:),"linewidth",2,'k-') ## axis([0 5]) P3=ones(1,NRx); logPmatrix=log(Pmatrix); k=6; ## Moving average for Bayesian estimation (6 days: incubation period) for i=1:N P3=exp(mavgmatrix(k*logPmatrix,k))(i,:); P3=P3/(eps+trapz(Rx,P3)); [jj ii]=max(P3); iRt(i)=ii; Rt(i)=Rx(ii); ## ############################################################ ## ## Highest density interval (HDI) calcs. 95%. ## ## Not the fasted algorithm, but ok... ## ############################################################ [jx ix]=min(abs(floor(10000*cumtrapz(Rx,P3))-5*100)); Rtm(i)=Rx(ix); [jx ix]=min(abs(floor(10000000000*cumtrapz(Rx,P3))-95*100000000)); RtM(i)=Rx(ix); ## ############################################################ endfor endfunction
function retval=mavgmatrix(n,k, alpha = 0) N=min(size(n)); #epidemic days if ischar (alpha) k=exp(1:k); else k=(1:k).^alpha; endif k=k/sum(k); retval=zeros(size(n)); for i=1:max(size(n)) for j=1:N if j<length(k) r=length(k)-j + 1:length(k); retval(j,i)= dot(n(1:j,i),(k(r)./sum (k(r)))); else retval(j,i)=dot(n(j-length(k)+1:j,i),k); endif endfor endfor endfunction
function retval=mavgrt(n,k,gamma) N=length(n); ration=shift(n,-1)./n; [m1,z] = filter(ones(1,k),k,[1:N].*log(ration)); [m2,z] = filter(ones(1,k),k,[1:N].^2); retval=(gamma+m1([1:N-1])./m2([1:N-1]).*[1:N-1])/gamma; end
Criado/Created: 15-04-2020 [15:57]
Última actualização/Last updated: 27-11-2024 [17:00]
For attribution, please cite this work as:
Charters, T., "Rt: previsões para que te quero": https://nexp.pt/ddr/Rt.html (15-04-2020 [15:57])
(c) Tiago Charters