Tiago Charters work gallery about contact

A equação logística: um bocadinho de matemática nunca fez mal a ninguém

O modelo logístico é um modelo matemático genérico que modela sistemas simples com mecanismos de feedback e que não têm apenas um comportamento trivial de crescimento. Modela o crescimento de bactérias em laboratório com espaço físico limitado e alimentação em quantidades finitas¹, a propagação de vírus como o COVID19, difusão de boatos numa comunidade, etc. É um modelo simples com uma larga banda de aplicabilidade.

O modelo logístico assume que o crescimento inicial de uma população com 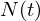indivíduos aumenta exponencialmente com taxa de crescimento inicial constante. À medida que 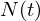se aproxima do limite máximo, só atingido assimptoticamente e a taxa de crescimento 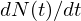diminui, o gráfico desta função fica com a forma de um S. Forma pela qual o modelo é facilmente reconhecido.

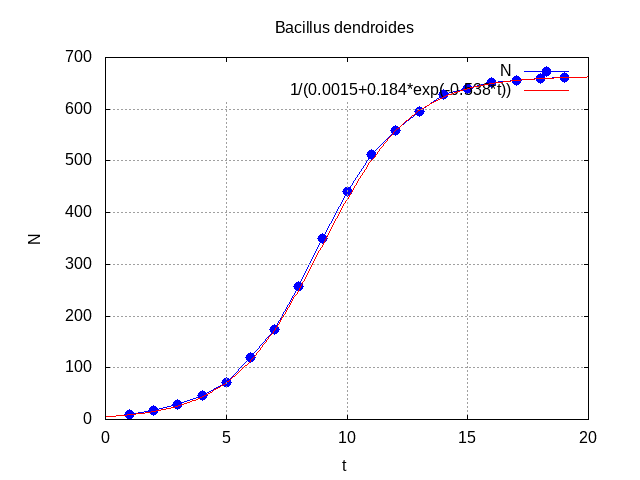
O caso clássico de aplicação deste modelo é o caso do crescimento da bactéria Bacillus dendroides¹² cuja evolução de crescimento se mostra na figura seguinte em três instantes.

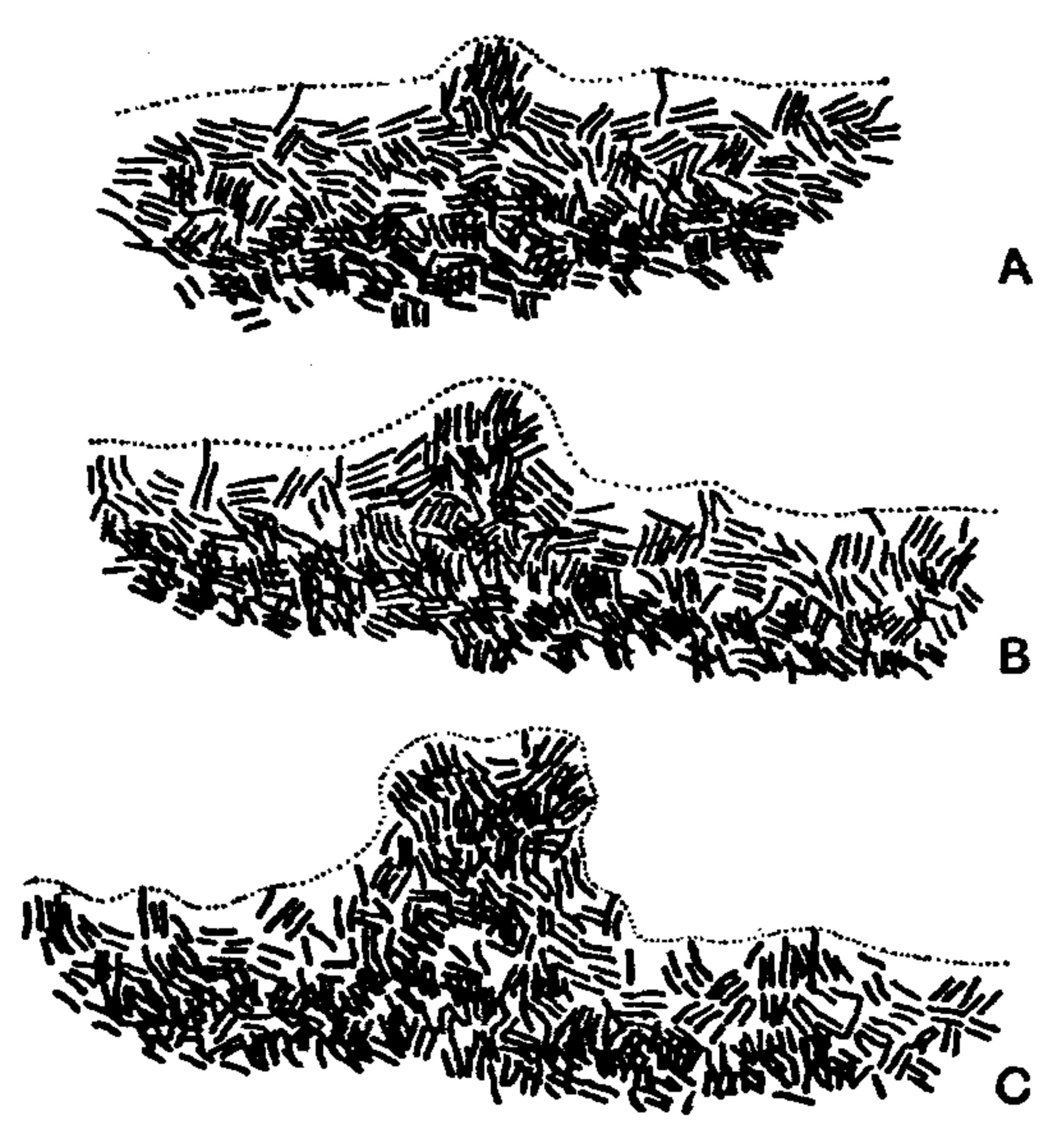
A figura seguinte mostra a azul os sucessivos estágios de desenvolvimento da bactéria Bacillus dendroides num período de 6 horas numa solução de agar-agar. Neste caso usa-se a área ocupada pelo crescimento como medida do número de B. dendroides em instantes sucessivos.

É possível modelar o crescimento de 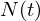indivíduos de uma determinada população através de uma equação diferencial, equação logística, com a forma

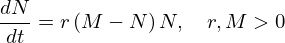
A solução da equação anterior com condição inicial 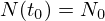(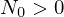) é dada por

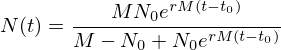
O valor 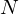atinge metade do valor máximo 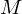no instante

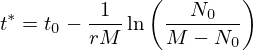
Outra forma de escrever a solução da equação e que é mais útil para estimar os parâmetros relevantes é³:

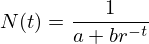
Foi esta a forma da equação usada para estimar e traçar a curva a vermelho do gráfico anterior usando o código em Maxima seguinte:

y:matrix(
  [0,9.6],
  [1,18.3],
  [2,29.0],
  [3,47.2],
  [4,71.1],
  [5,119.1],
  [6,174.6],
  [7,257.3],
  [8,350.7],
  [9,441.0],
  [10,513.3],
  [11,559.7],
  [12,594.8],
  [13,629.4],
  [14,640.8],
  [15,651.1],
  [16,655.9],
  [17,659.6],
  [18,661.8])$


n:lmax(matrix_size(y))$
M:lmax(makelist(y[i][2],i,n))$
Y:makelist(1/y[i][2],i,n)$
/* m:1; */
m:3;
m:if evenp(m)then m+1 else m$

R:float(sum(Y[i],i,1,m)/m)$
T:float(sum(Y[n-i],i,0,m-1)/m)$
S:if evenp(n)
  then
  sum(Y[n/2+i]/m,i,-(m-1)/2,(m-1)/2)
  else
  sum(Y[(n+1)/2+i]/m,i,-(m-1)/2,(m-1)/2)$

aux:if evenp(n)then 1 else 0$
r:exp(2/(n-m-aux)*log((T-S)/(S-R)))$

nx:if evenp(n)then n/2 else (n+1)/2$
[ax+bx*(r^((m+1)/2)+r^(n-(m+1)/2))/2=(T+R)/2, ax+bx*r^nx=S]$
solab:float(solve(%,[ax,bx]))$
a:(rhs(solab[1][1]))$
b:(rhs(solab[1][2]))$

P(t):=1/(a+b*r^(t))$
k:log(1/r)$
Pe(t):= 1/(a+b*exp(-k*t))$
nstar:ceiling(log(abs(-a/b))/log(r))$

ap:float(floor(100000*a)/100000);
bp:float(floor(1000*b)/1000);
kp:float(floor(1000*k)/1000);

aps:string(ap);
bps:string(bp);
kps:string(kp);

tplot:"Bacillus dendroides";

nfinal:n+3;
plot2d([[discrete, args(1/Y)],P(t)],
  [t,0,nfinal],
  [title,tplot],
  [xlabel, "t"],
  [ylabel, "N"],
  [style, linespoints, lines],
  [legend, Legend[1][1], concat("1/(",aps,"+",bps,"*exp(-",kps,"*t))")],
  grid2d)$

baseado no trabalho de Mar-Molinero com título Tractors in Spain: A Logistic Analysis ³.

1. R. Pearl, ‘‘The Growth of Population’’ Quart. Rev. Biol. 2, 532–548, (1927)

2. H. G. Thornton, On the development of a standardized agar medium for counting soil bacteria Ann. Appl. Biol., 9:241-274, (1922)

3. C. Mar-Molinero, Tractors in Spain: A Logistic Analysis, The Journal of the Operational Research Society, Vol. 31, No. 2, pp. 141-152 (1980)

---

Back...

---

For attribution, please cite this work as:

Charters, T., "A equação logística: um bocadinho de matemática nunca fez mal a ninguém": https://nexp.pt/ddr/bd19.html (11-03-2020 [16:56])

(c) Tiago Charters