Parábolas para que te quero
Todos os dias, a meio do dia, recebemos o relatório da Direção Geral de Saúde sobre o desenvolvimento da epidemia do COVID19 em Portugal. Dois números são normalmente destacados nos órgãos de comunicação social e nas redes sociais. São eles o número total de infectados, N, e a variação desse número relativamente ao dia anterior, dN/dt. São números importantes, são duas quantidades relevantes para a descrição da propagação da epidemia porque a equação do movimento epidémica relaciona estas duas quantidades.
A figura seguinte mostra o modelo e a relação entre essas duas quantidades. Corresponde ao mais simples modelo que podemos construir para perceber e estudar a evolução da epidemia: modelo logístico.
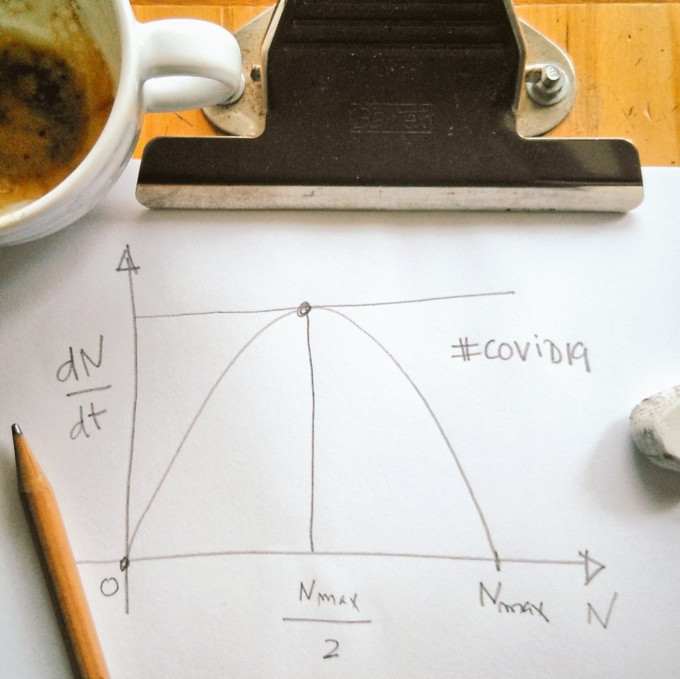
A solução da equação que relaciona estas duas quantidades permite fazer previsões sobre a dinâmica deste fenómeno que é um fenómeno natural. Essa equação é uma lei do movimento para este tipo de fenómenos de crescimento nos quais os acontecimentos epidemiológicos se enquadram. Não são os únicos. As curvas de evolução são uma curva-tipo-S, sigmóides: têm um crescimento rápido inicial e depois um plateau final, assimptótico. Este modelo simples permite fazer estimativas analíticas sobre o comportamento epidémico. Usualmente as previsões feitas com este modelo dão-nos um lower bound para a os parâmetros estimados.
A taxa de crescimento do número de infetados num dado dia é proporcional ao valor do número de infetados nesse dia. Isto acontece quando o número de infetados é pequeno relativamente ao número total final de infetados. Este número total final de infetados é por agora desconhecido mas, à semelhança do voo parabólico de uma bola atirada ao ar, em que a altura máxima determina o valor final da distância percorrido, à medida que a epidemia se vai desenvolvendo mais perto estamos desse valor extremo que corresponde neste caso ao dia onde a taxa de infeção é máxima. O vértice da parábola. Enquanto estivermos longe desse dia a epidemia desenvolve-se num regime de crescimento (quasi)exponencial.
Quando o número de infetados num dia atinge os 10% do número total a evolução deixa de ser "exponencial". A evolução continua a acelerar até atingir o máximo da taxa de infetados por dia e atinge um pico. A partir desse dia segue-se outro intervalo de tempo que nos leva aos 90% do número total de infetados. A duração d desse intervalo de tempo, que corresponde ao aumento de 10%-90%, é chamado tempo característico e depende unicamente do valor da taxa de crescimento exponencial k. É igual a ln(81)/k.
Atingido os 90% do número total de infetados a evolução estabiliza num plateau que corresponderá assimptoticamente ao número final de infetados.
E assim se constrói a curva-tipo-S.
É a propriedade do desenvolvimento parabólico da epidemia, o facto de que a metade do caminho podemos saber qual o número total de infetados, que nos permite prever ou estimar esse número final. Tal como a posição da bola no voo parabólico em que o ponto de altura máxima determina a distância total percorrida também o valor do número de infetados no momento onde a taxa número de infetados por dia é máxima determina o número final total de infetados. Aqui não temos força gravítica mas temos o número básico de reprodução que controla a taxa de crescimento exponencial da epidemia que é diferente, em geral, para diferentes vírus.
Vários ajustes parabólicos para diferentes países
Nota: Os dados têm um atraso de um dia devido à atualização da fonte: https://www.ecdc.europa.eu/en/geographical-distribution-2019-ncov-cases
Portugal
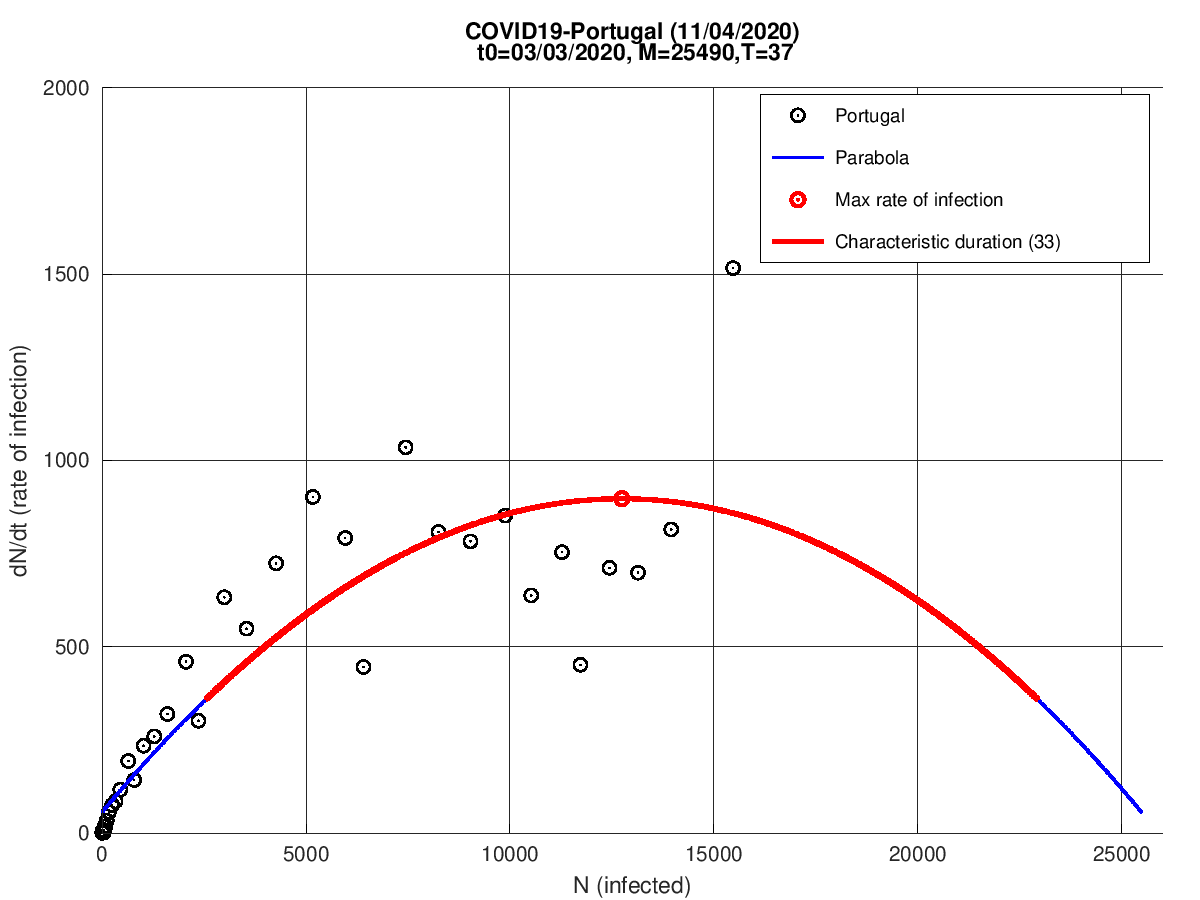
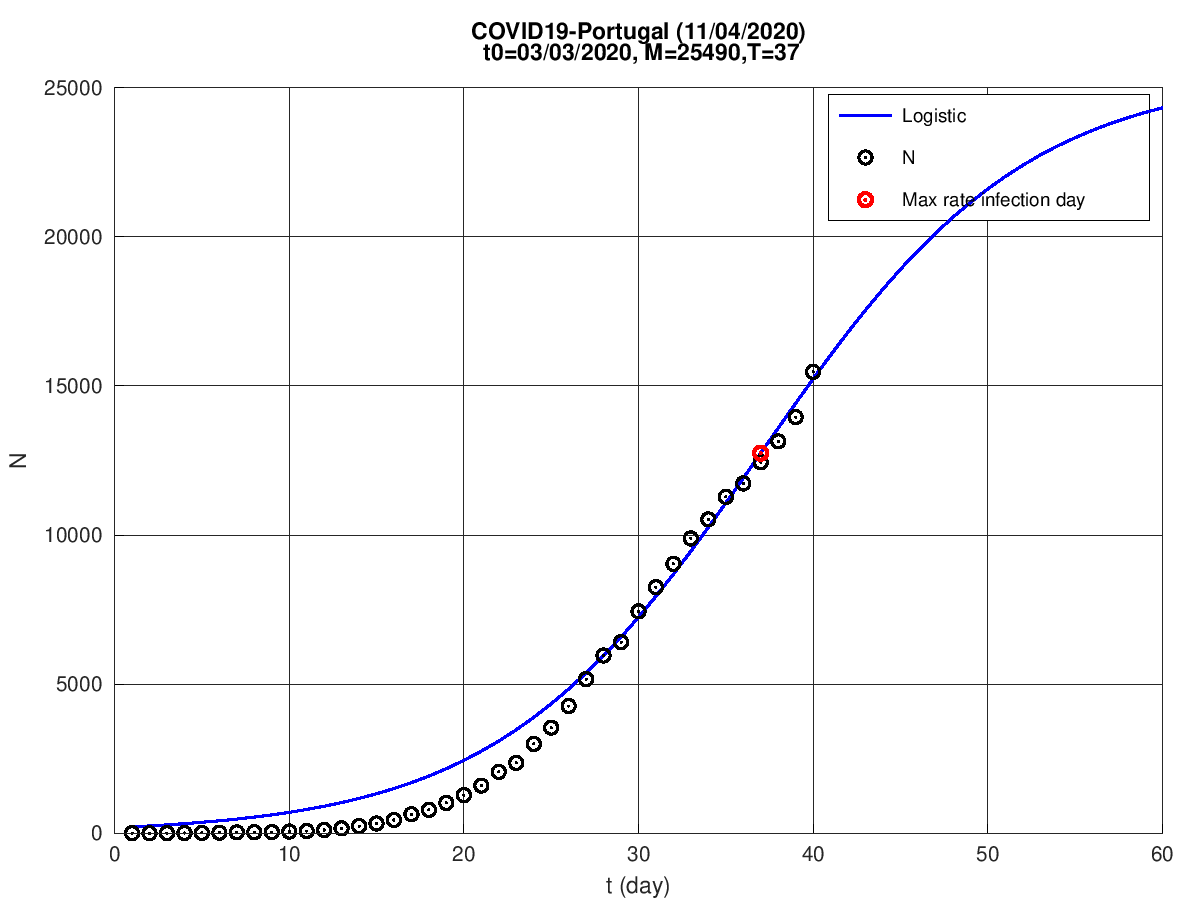
Itália
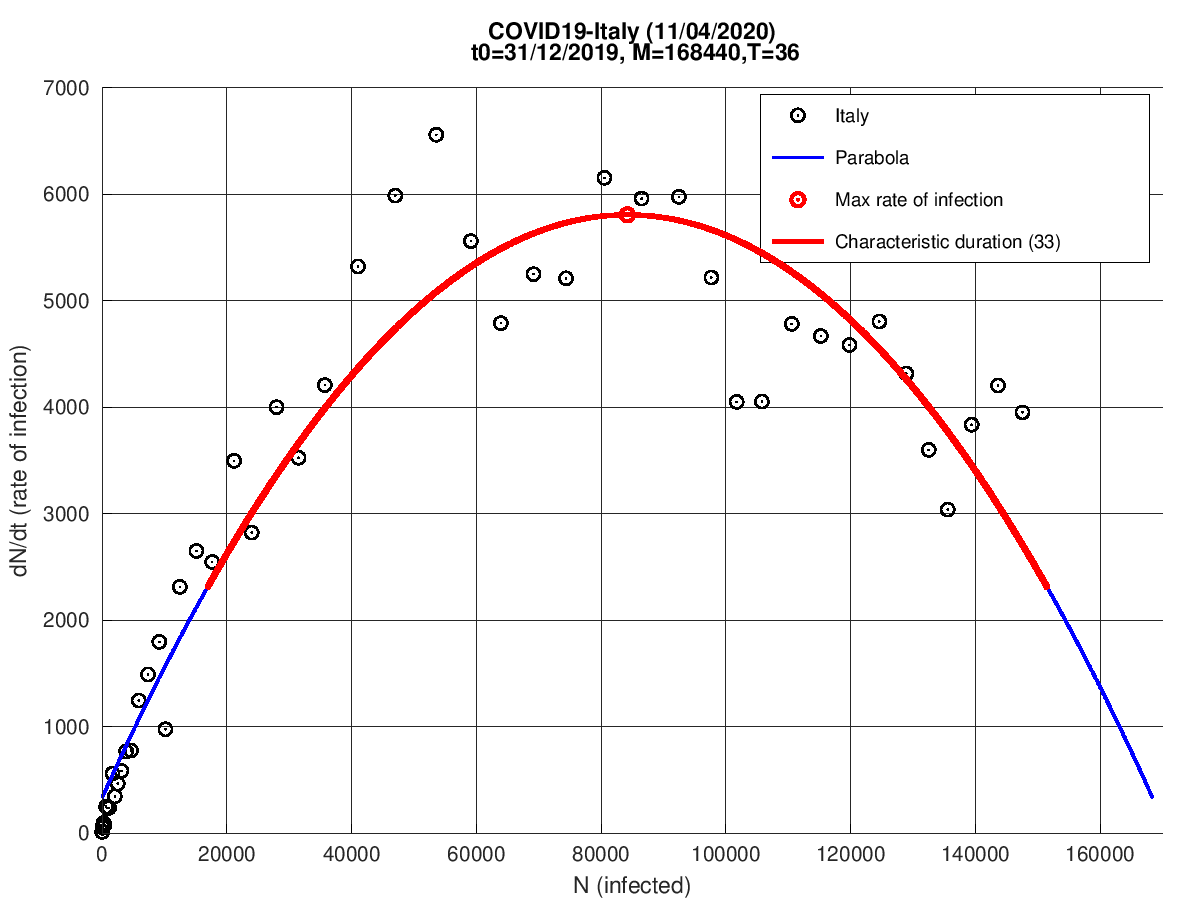
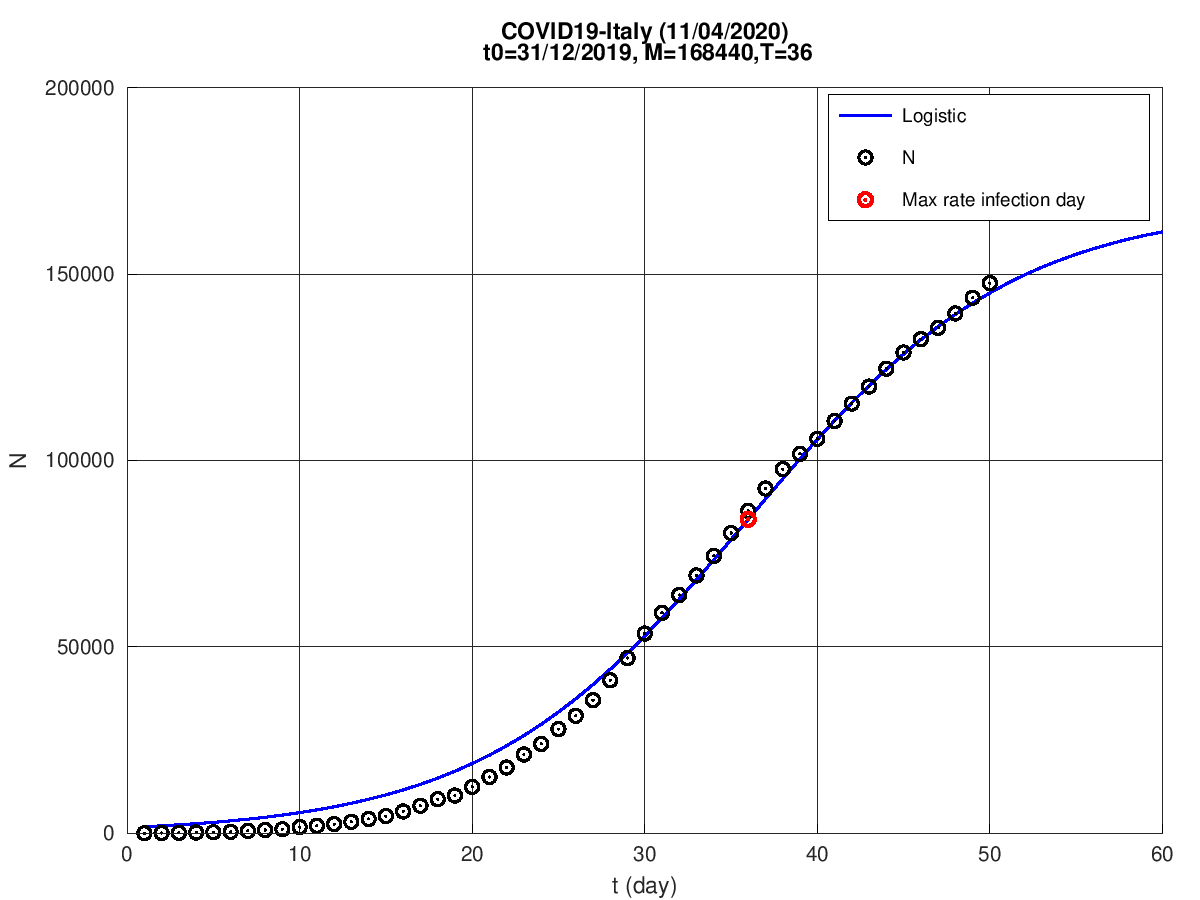
Espanha
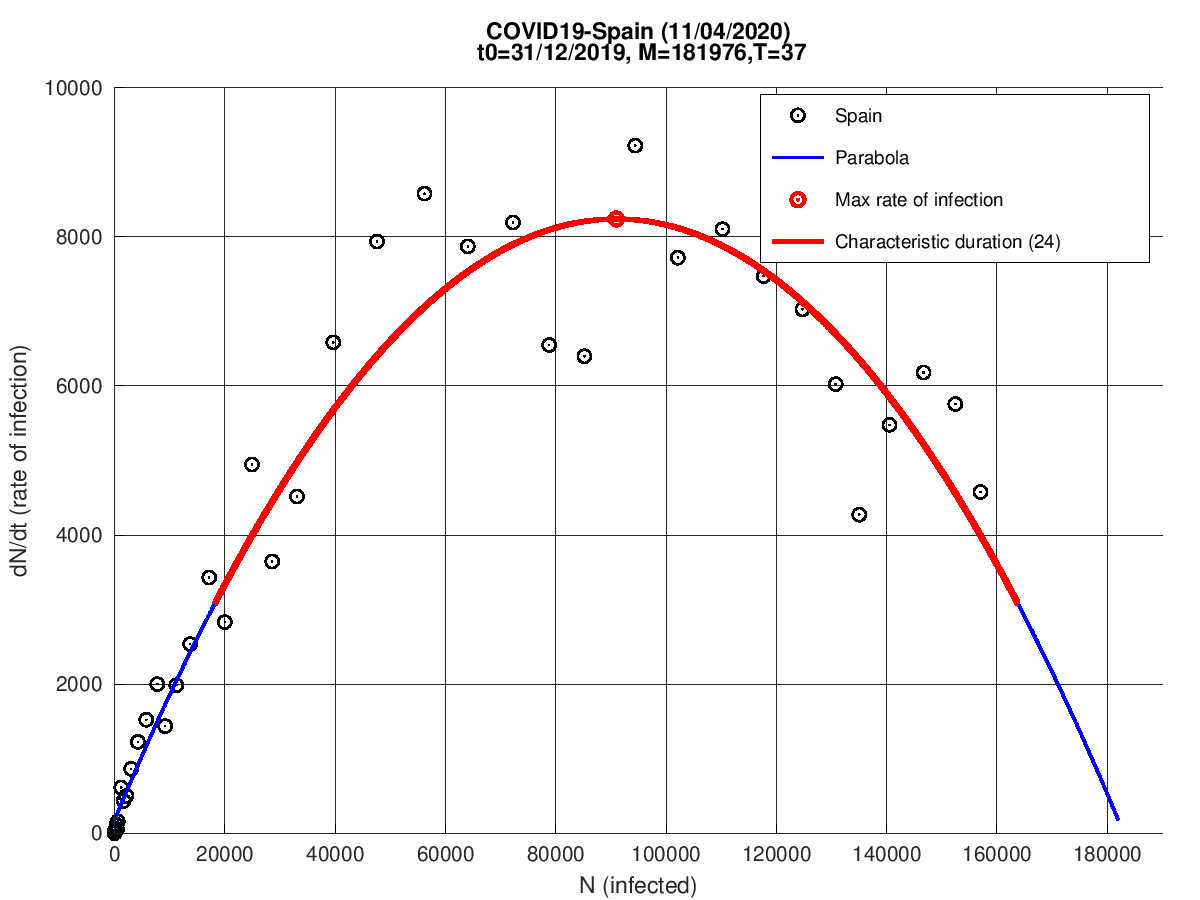
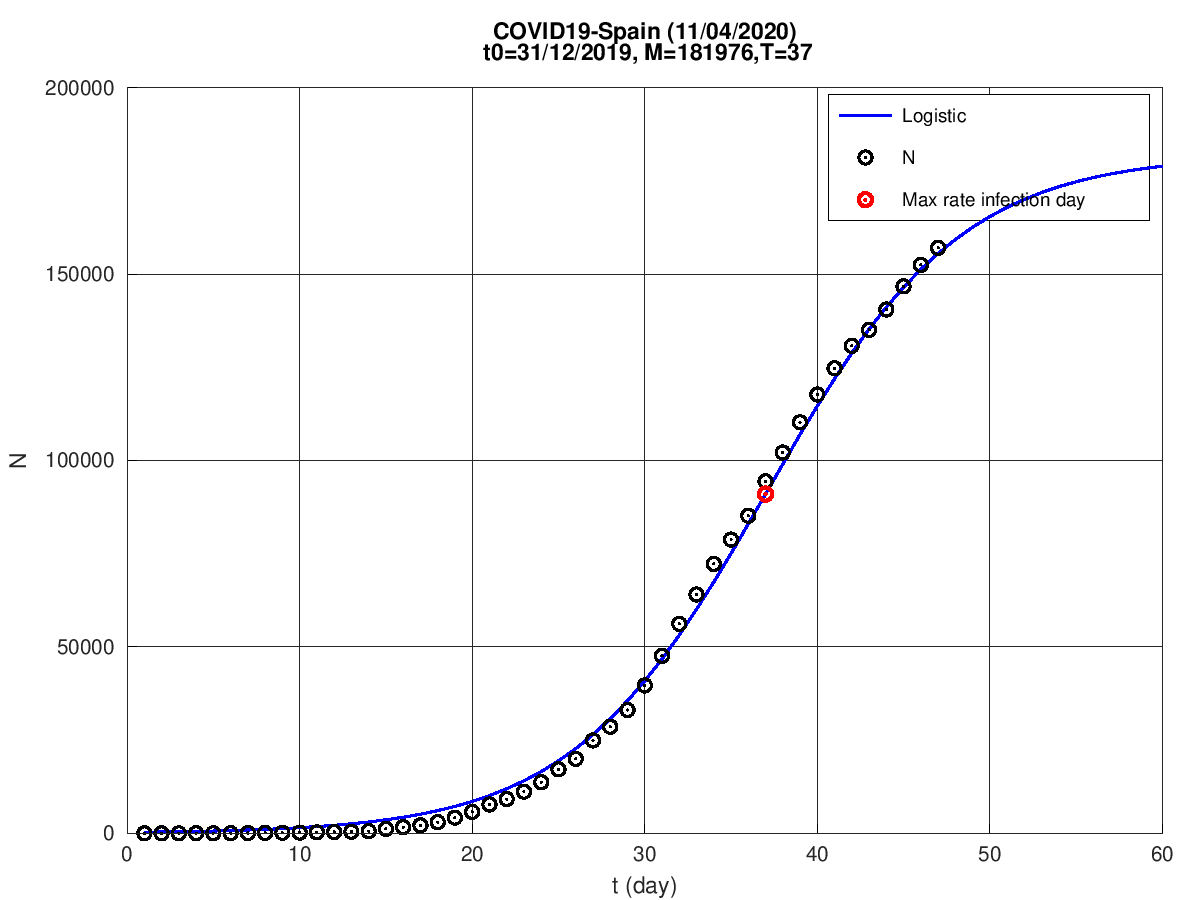
Alemanha
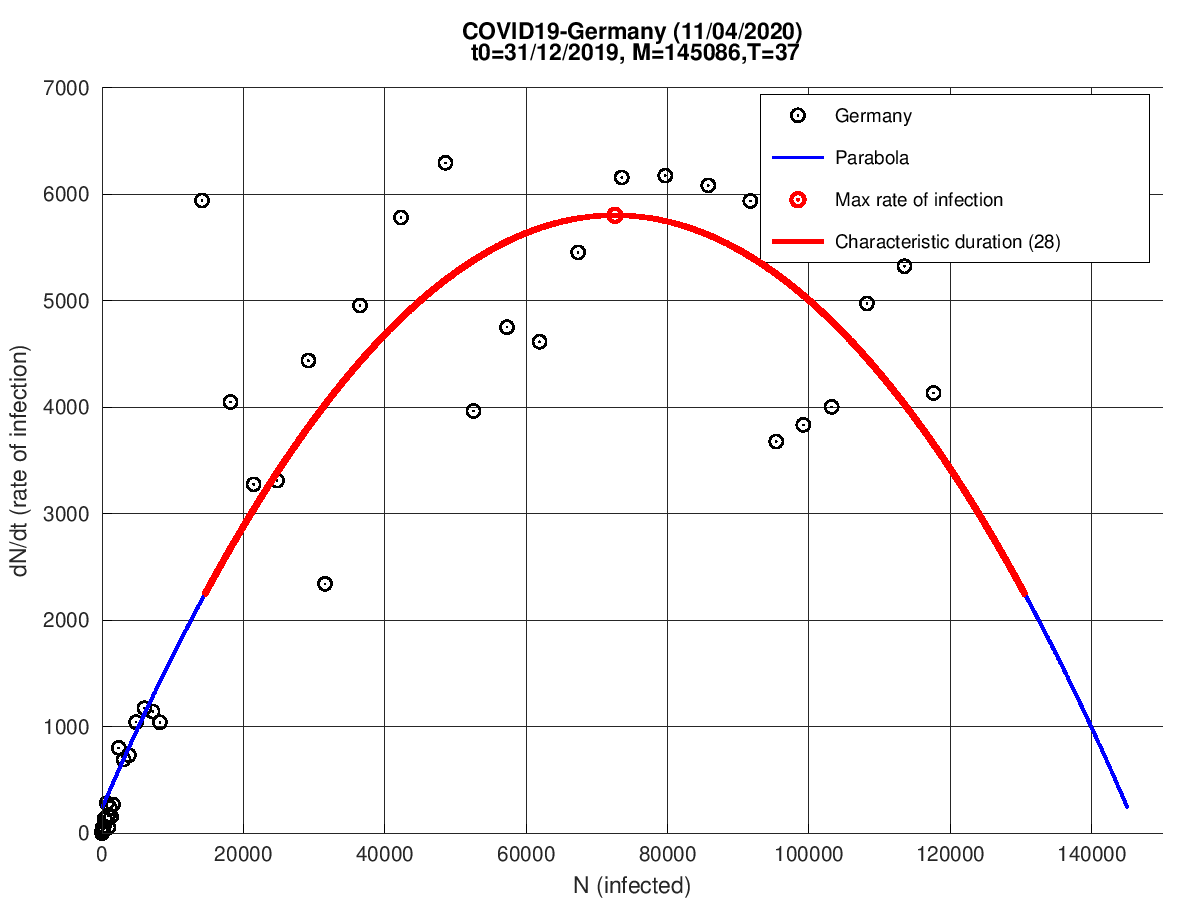
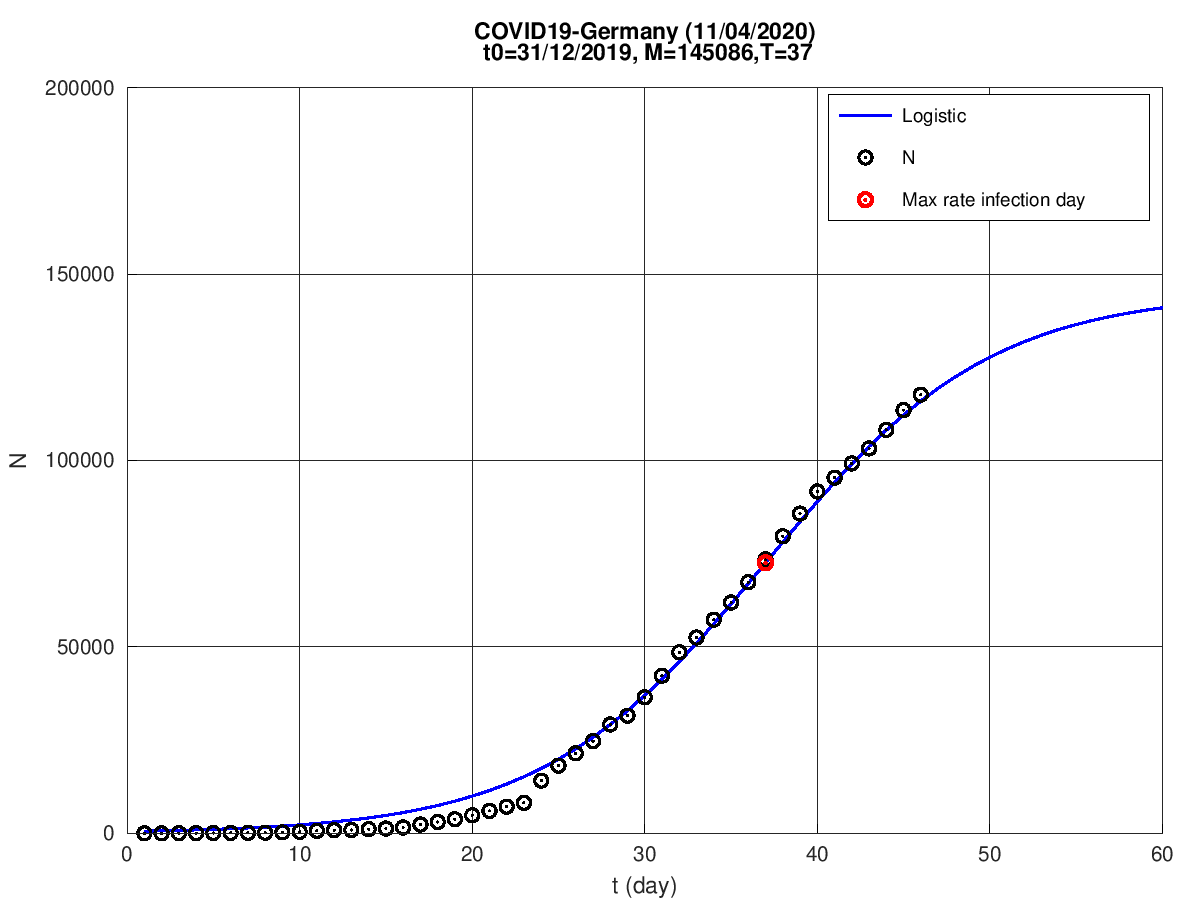
Suíça
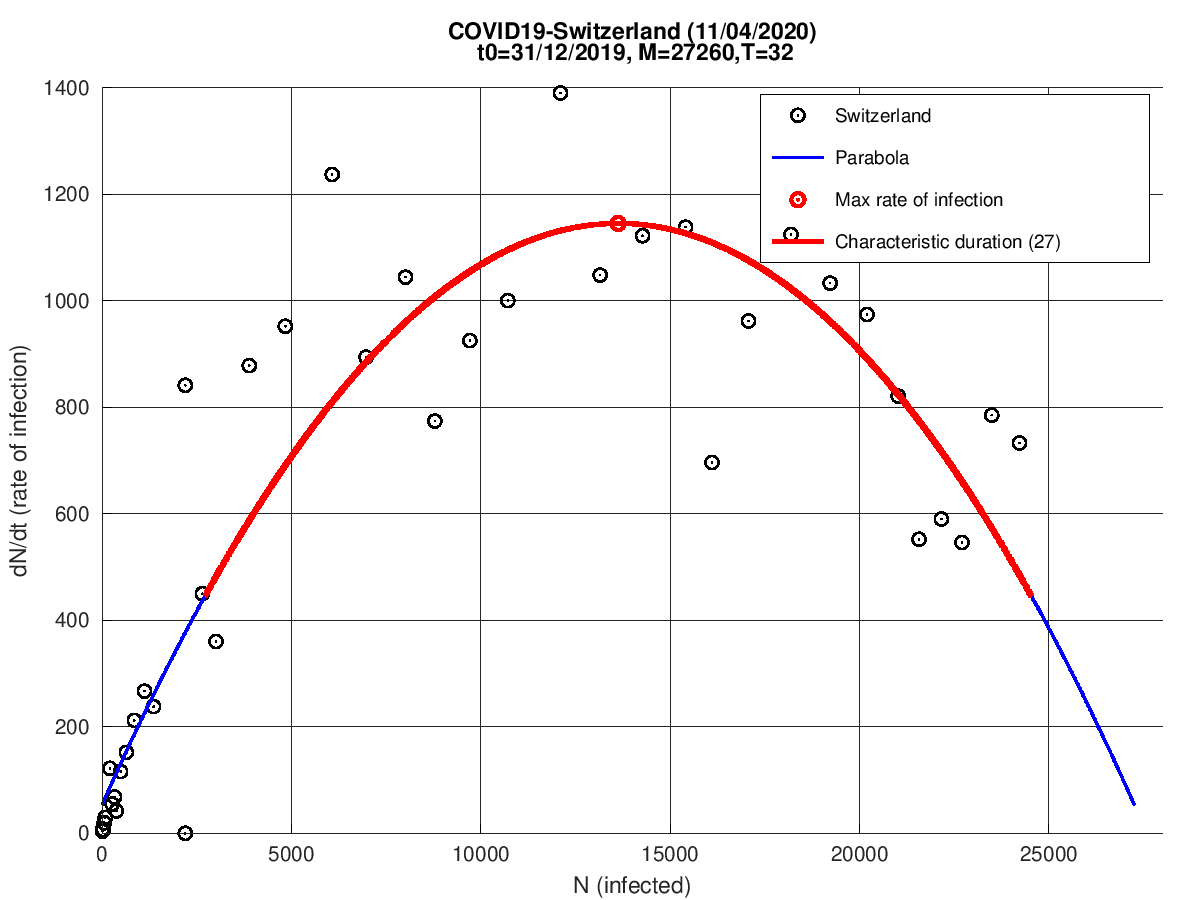
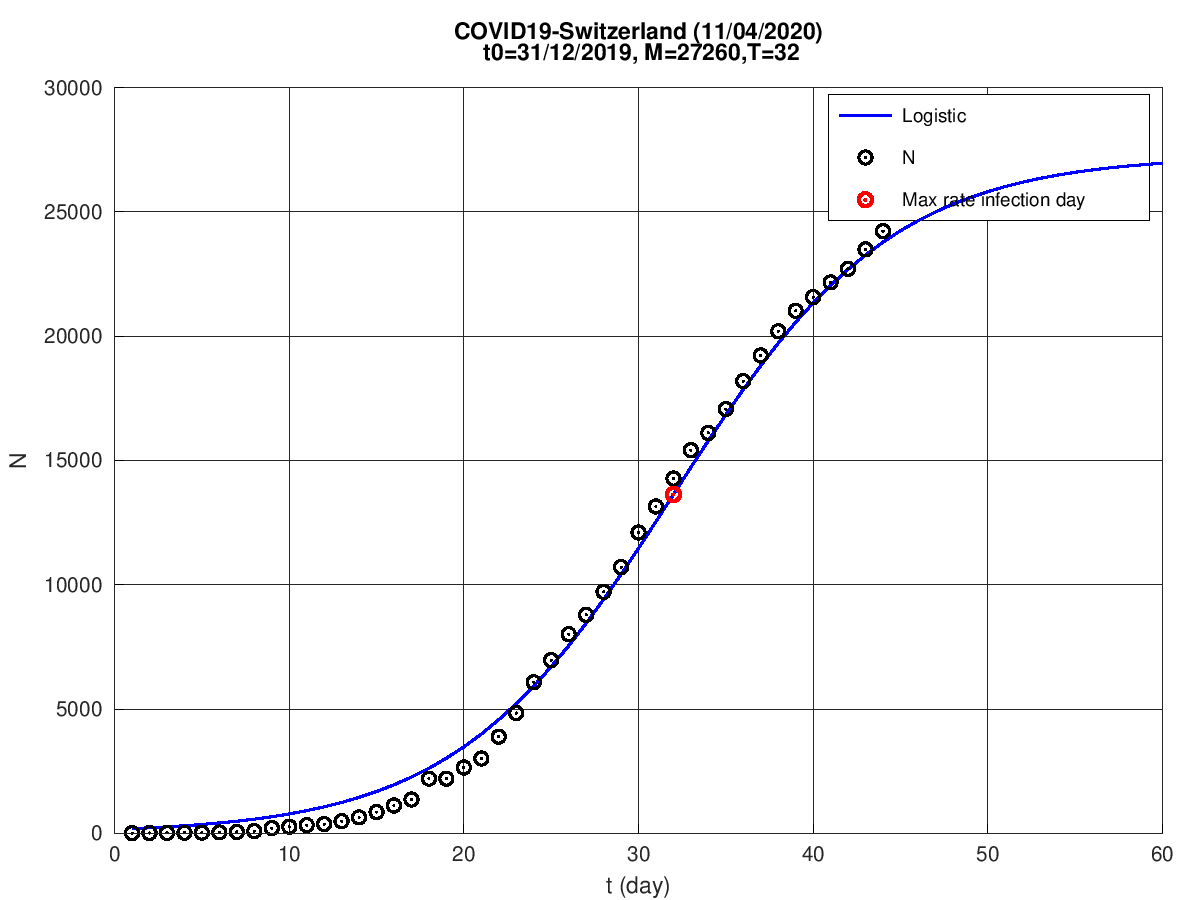
Suécia
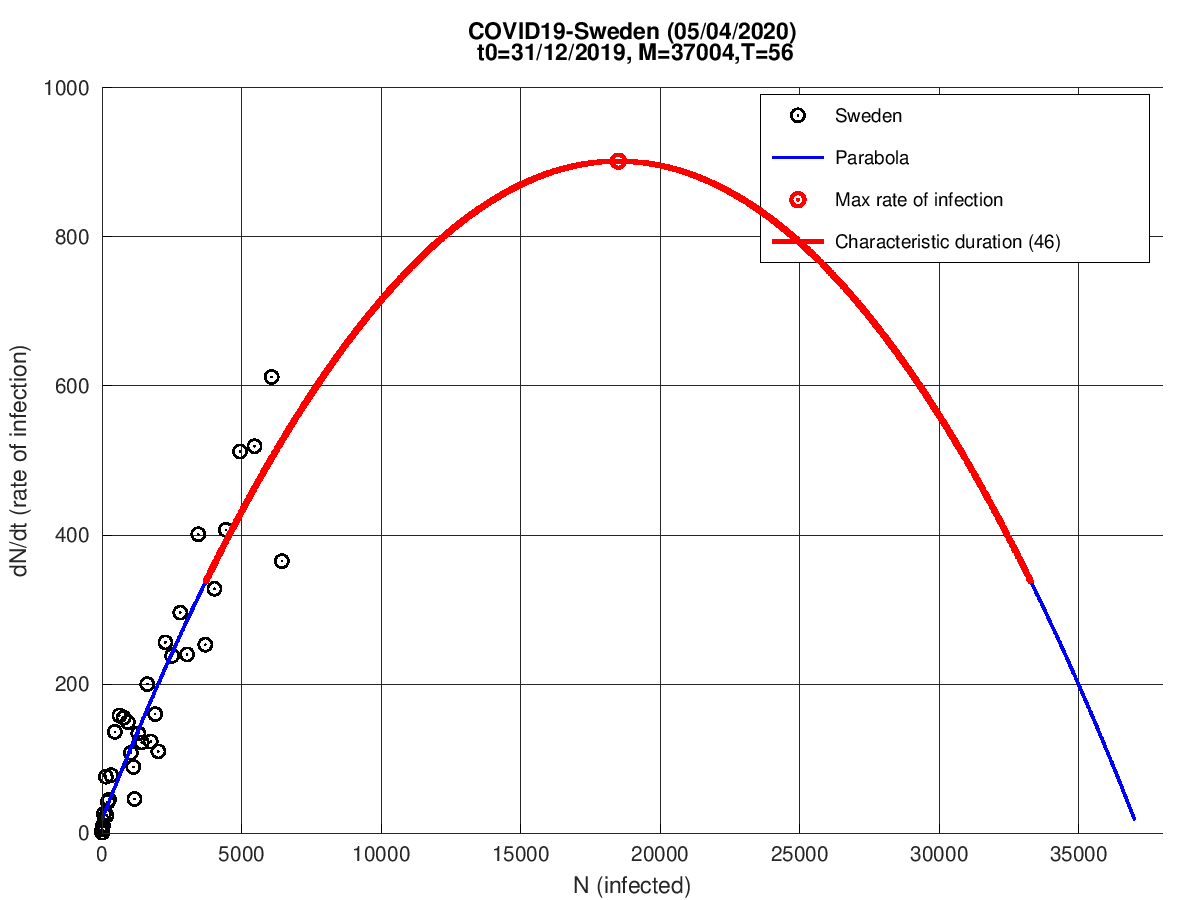
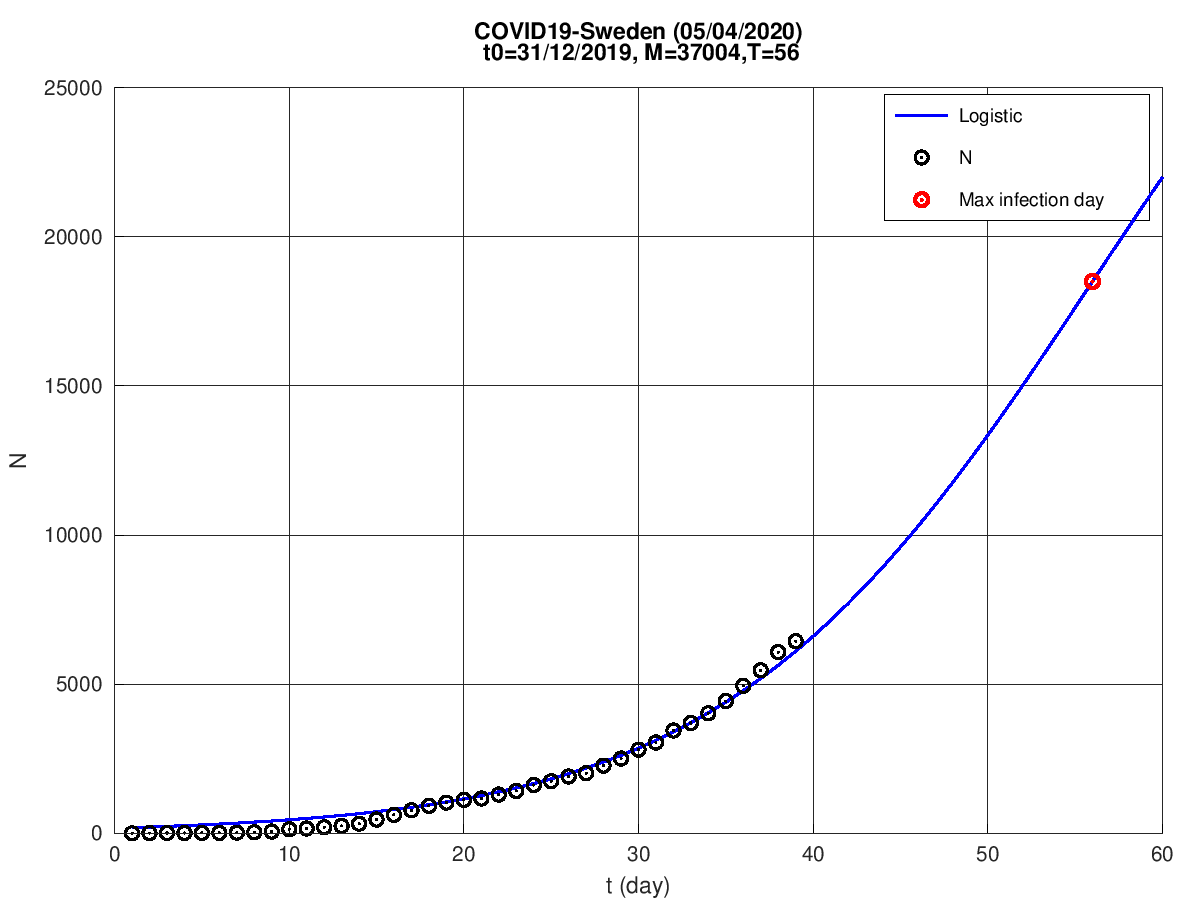
França
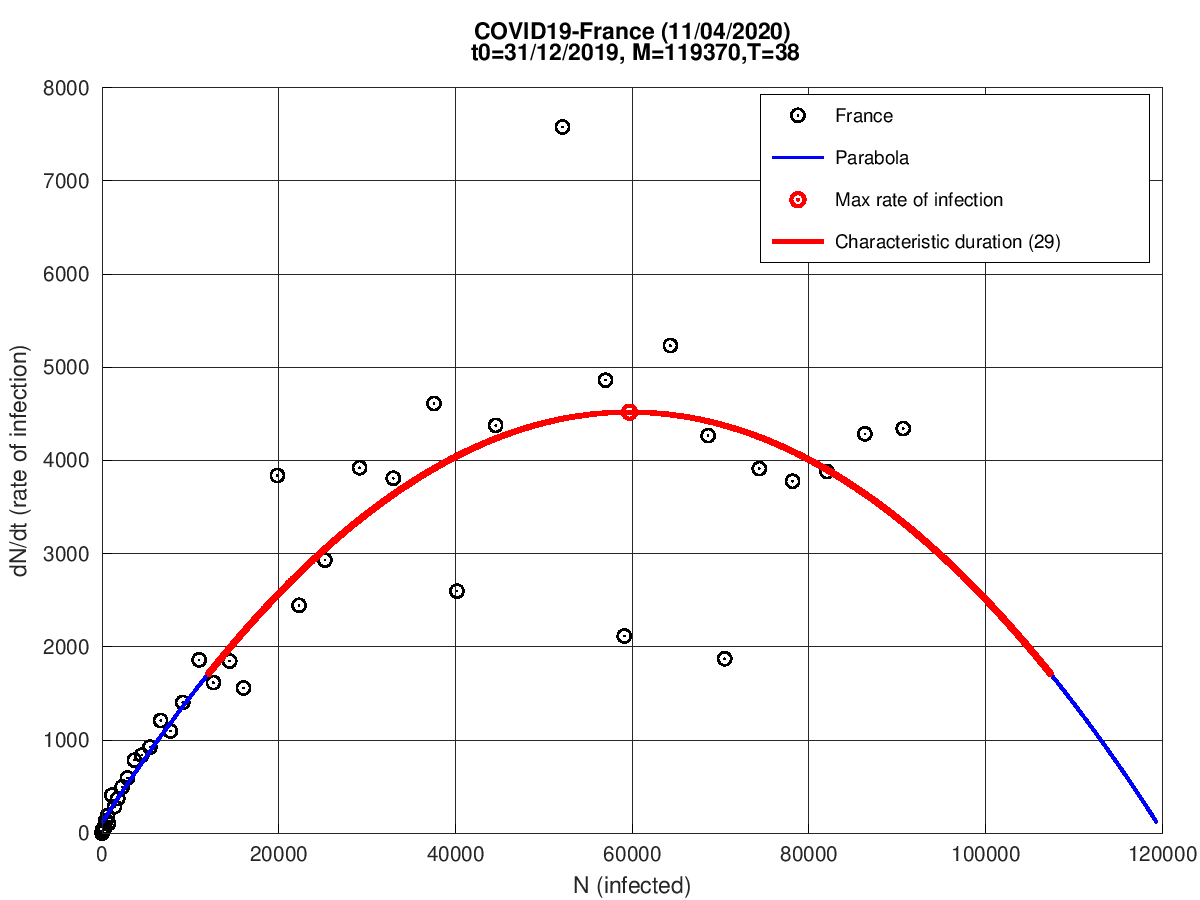
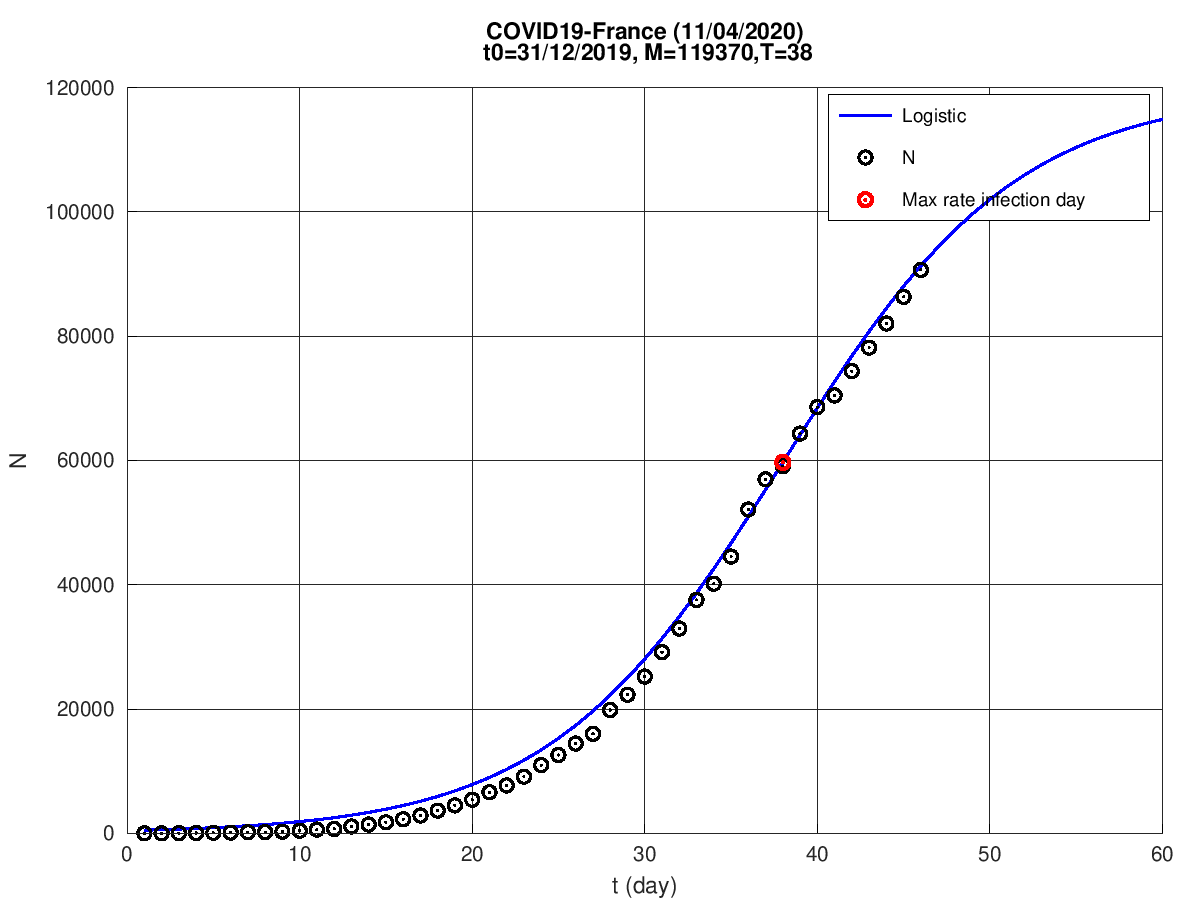
Reino Unido
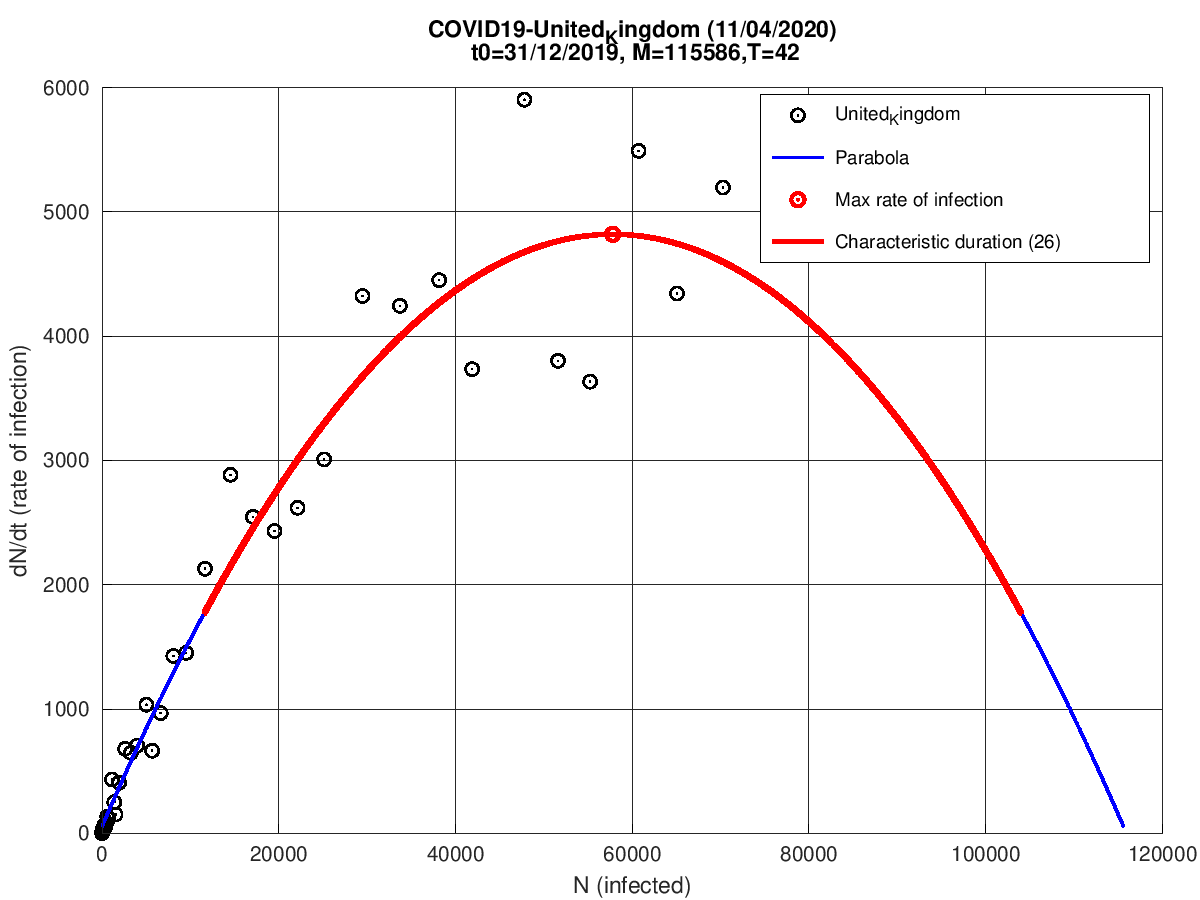
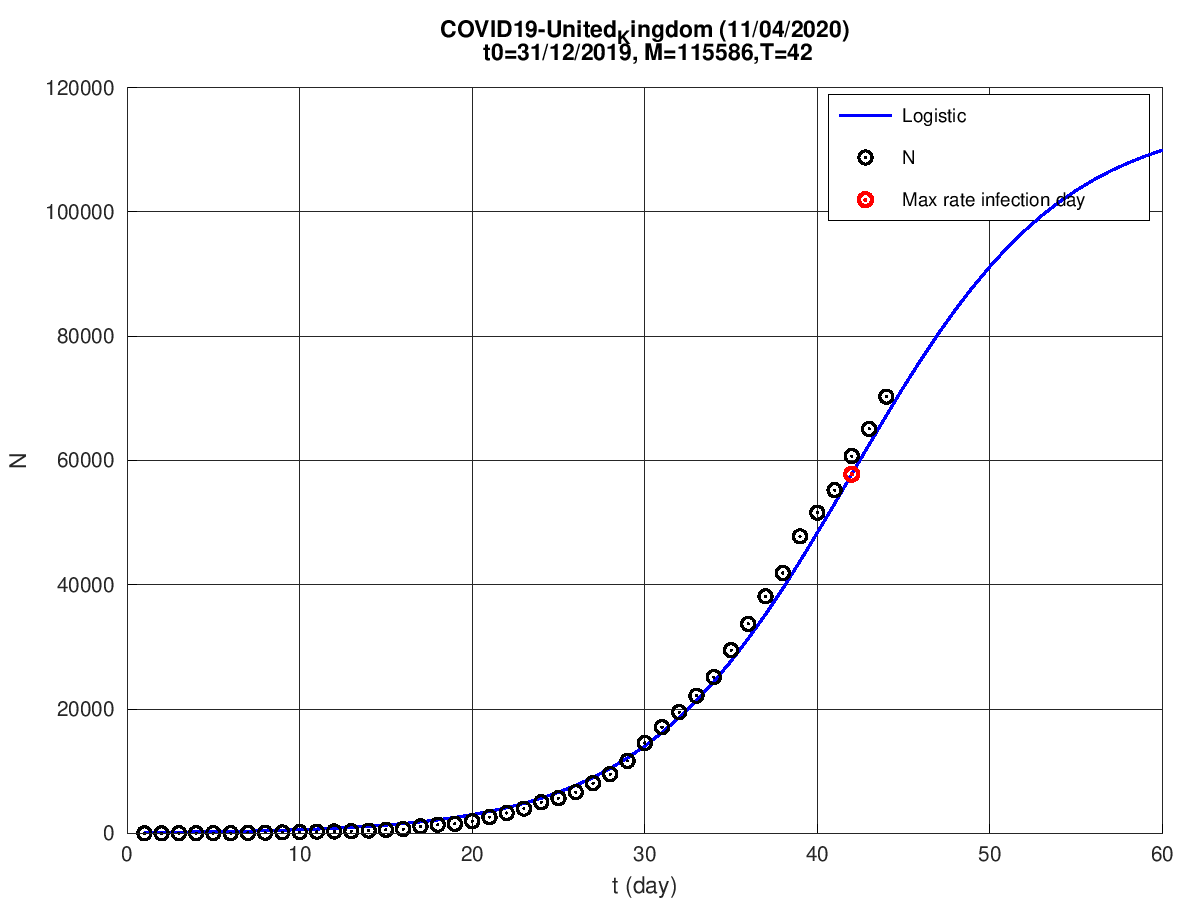
Bélgica
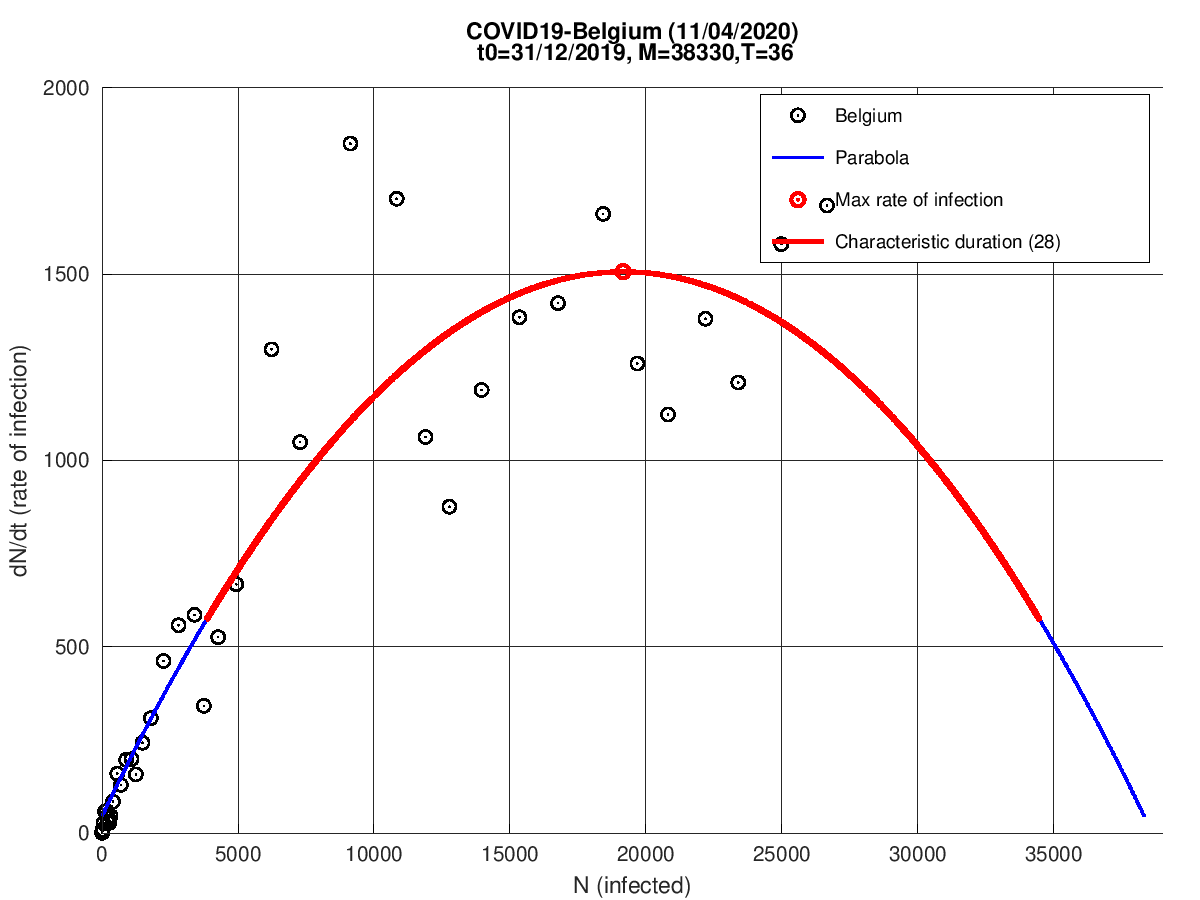
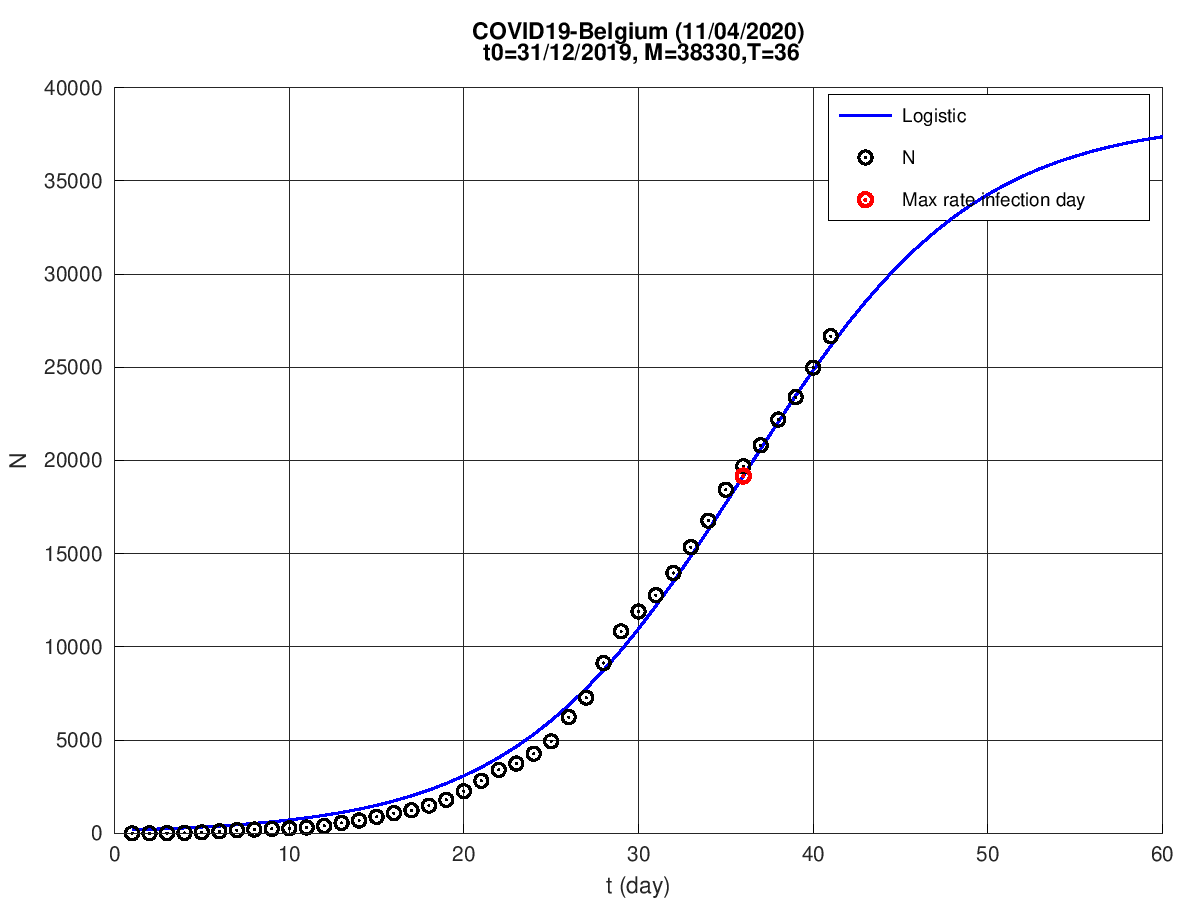
Holanda
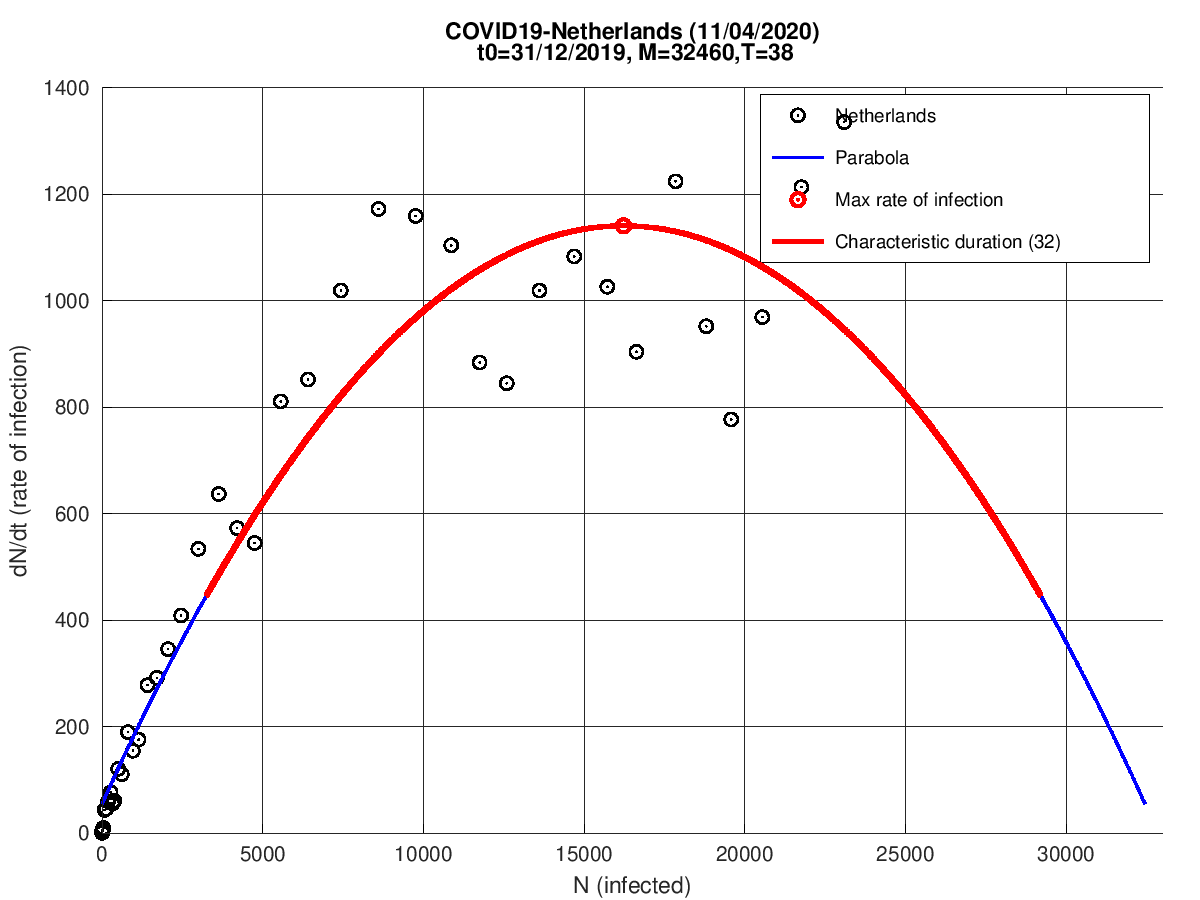
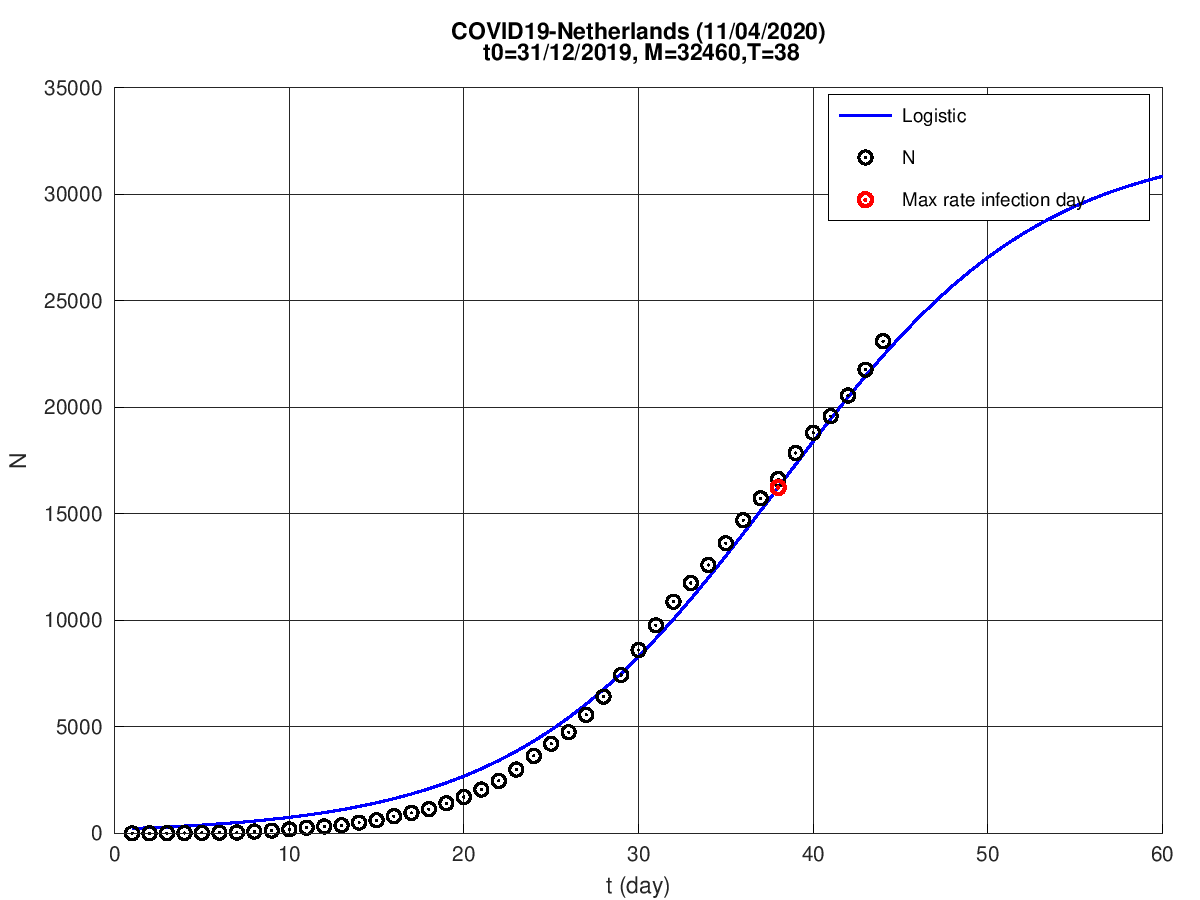
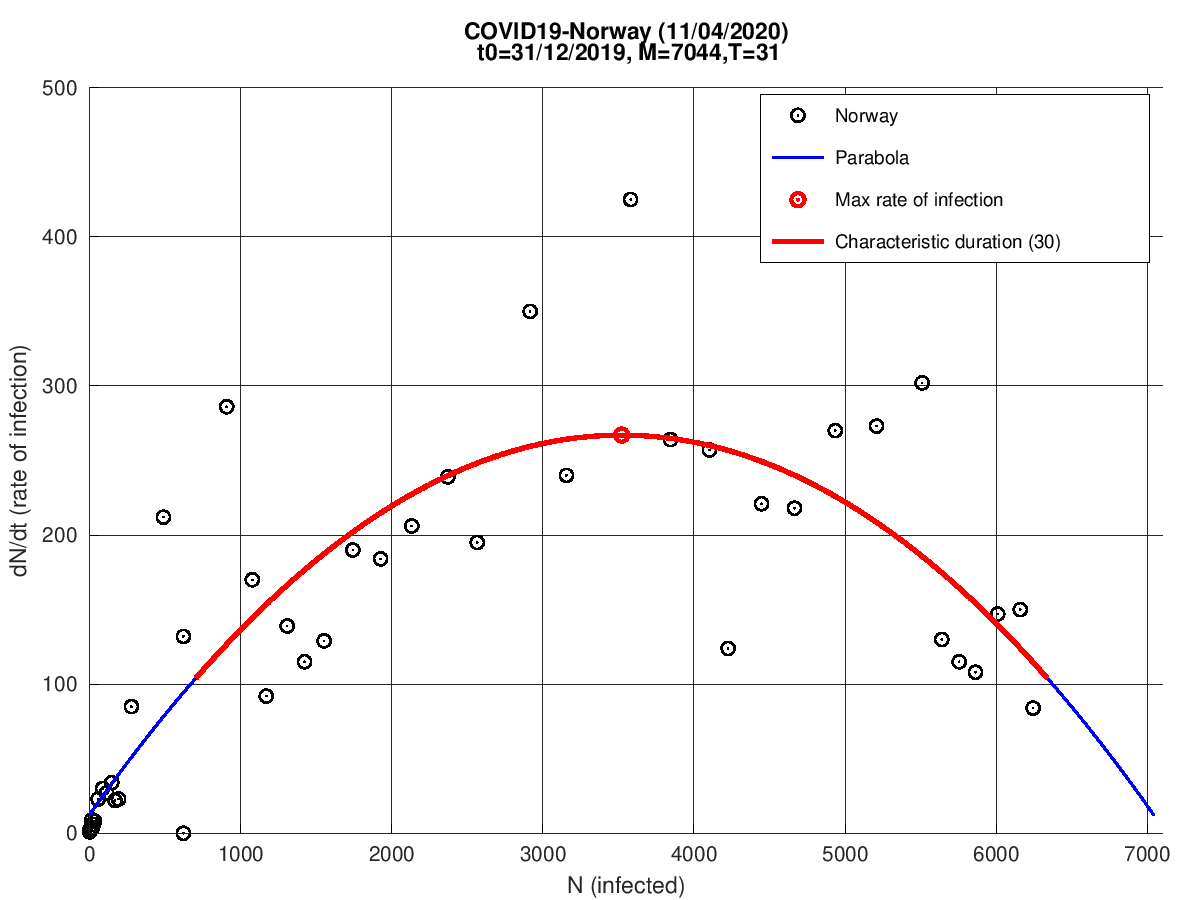
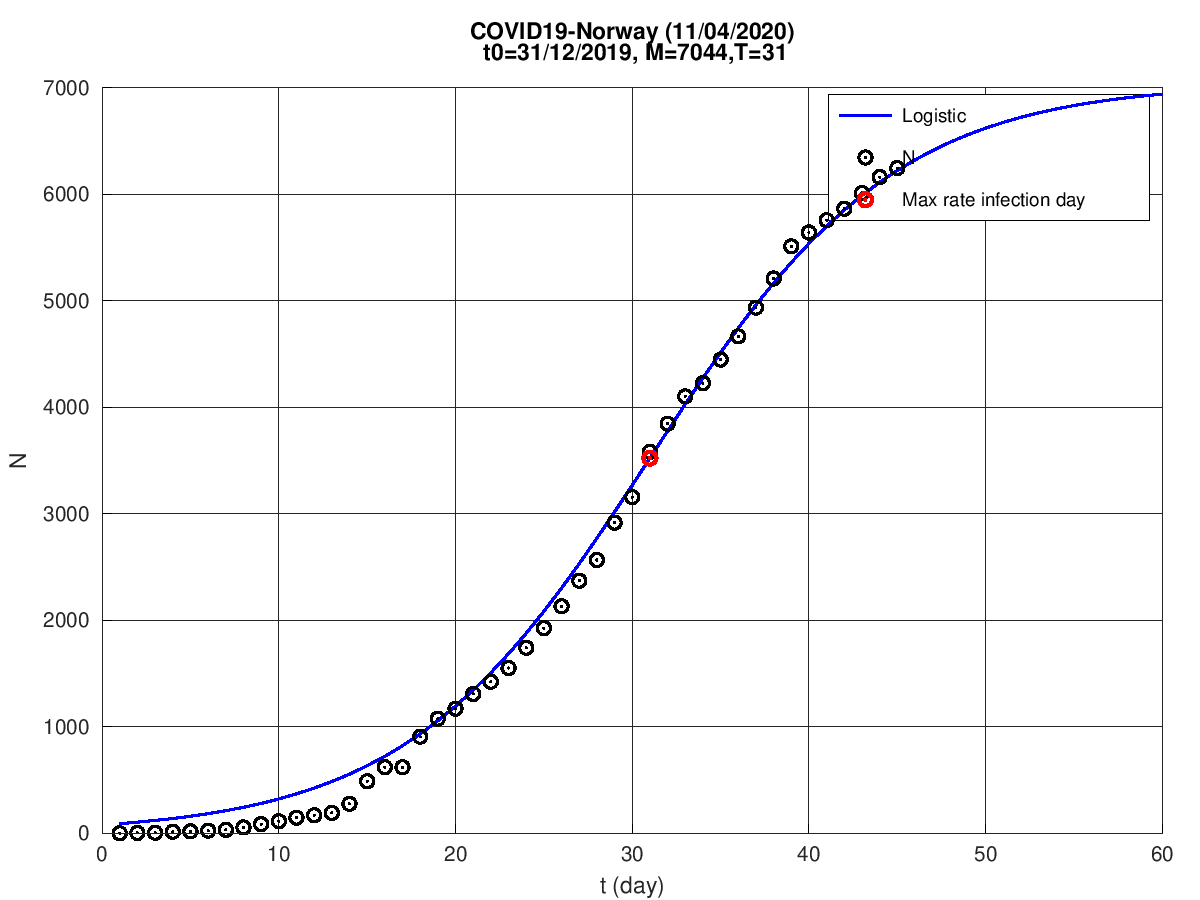
Noruega
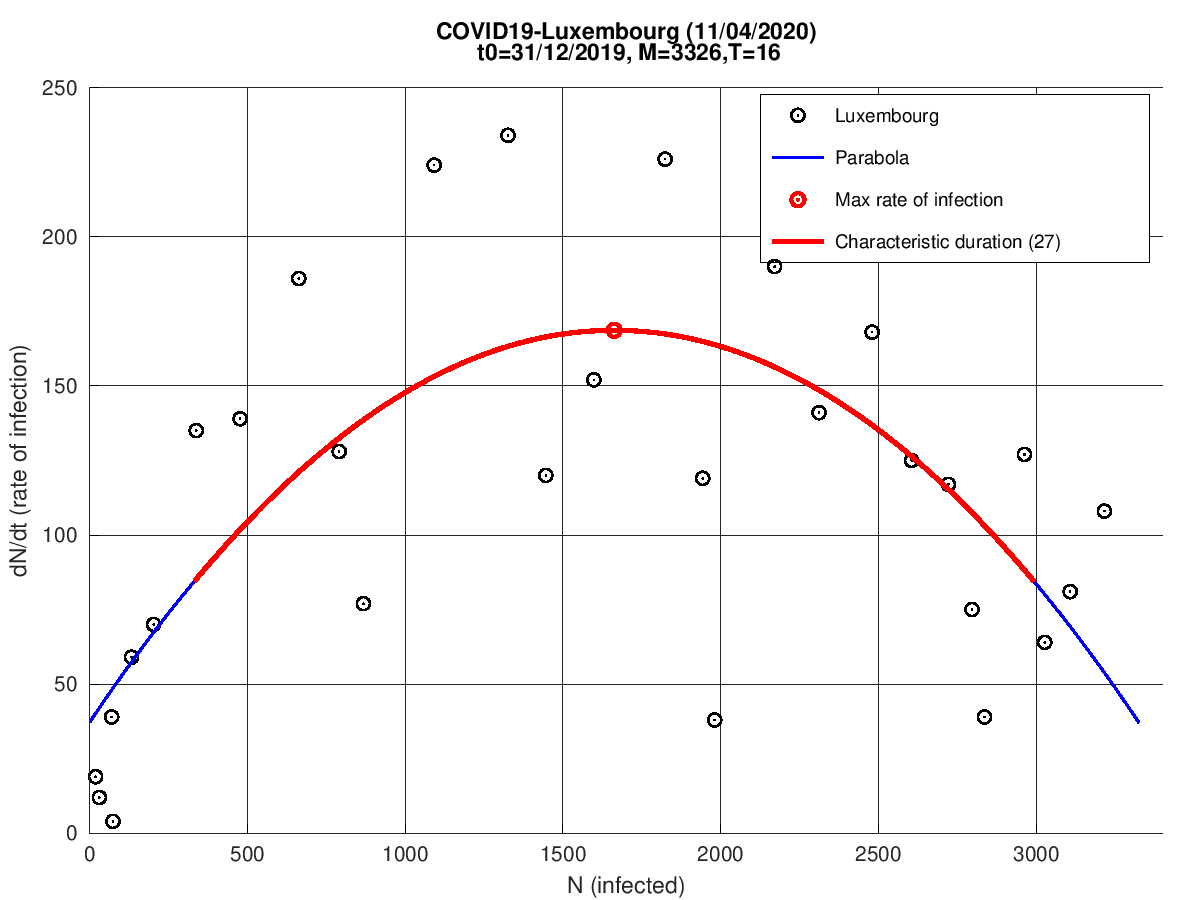
Luxemburgo
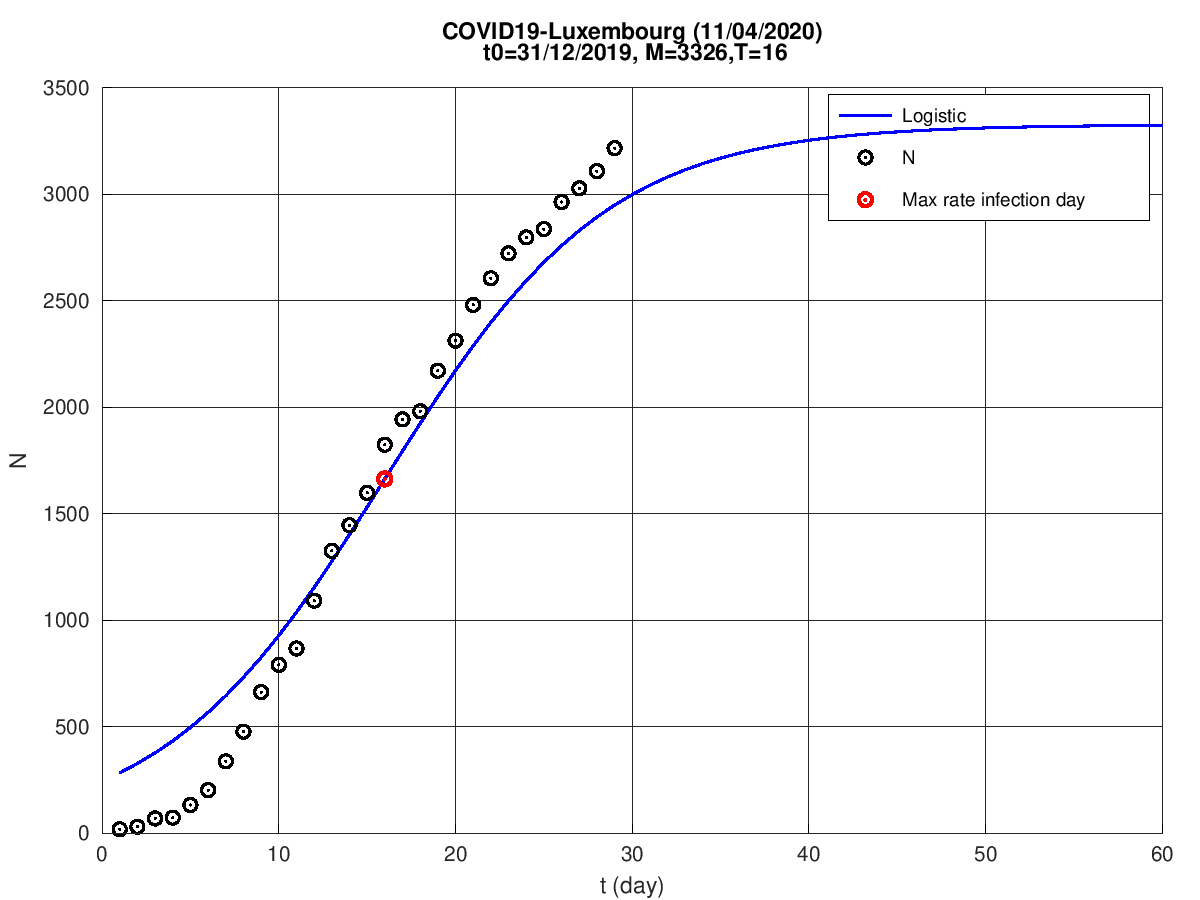
Filândia
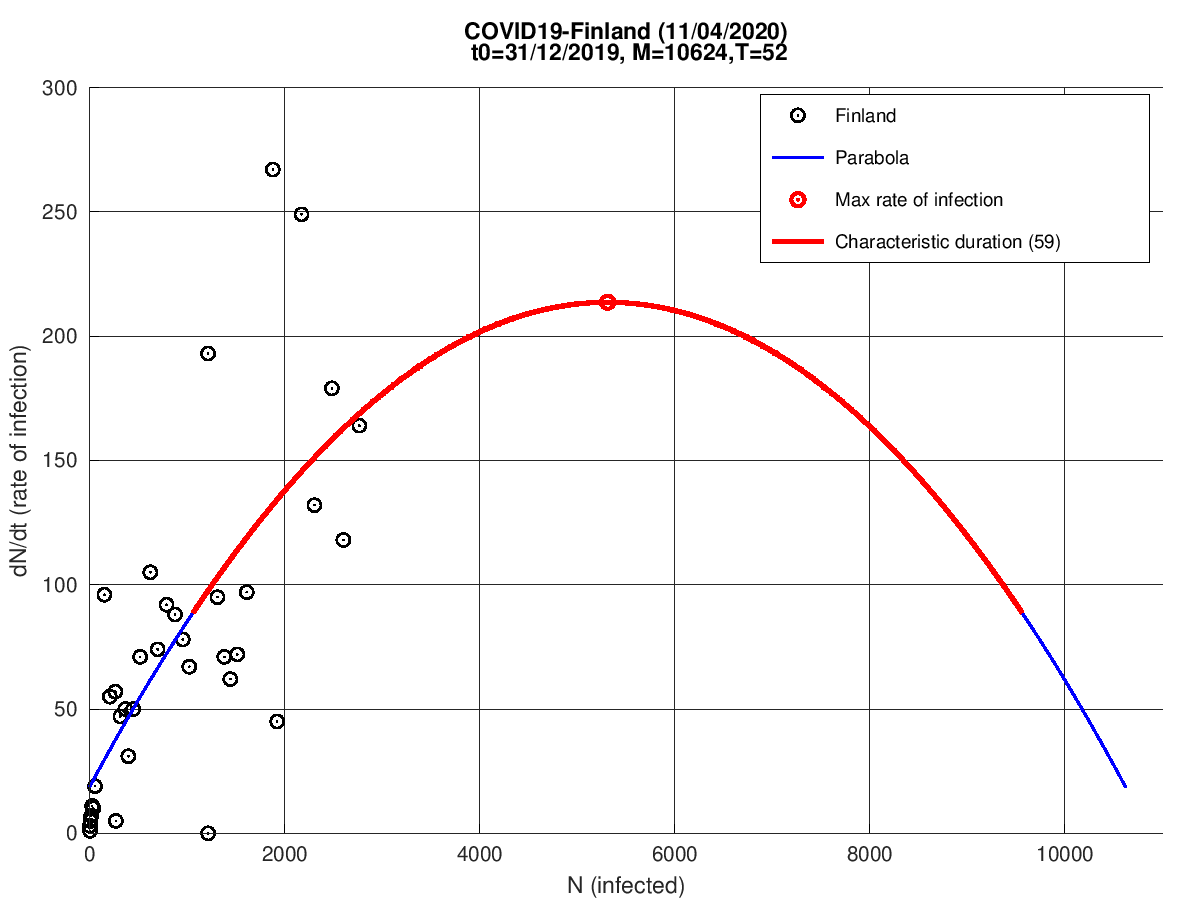
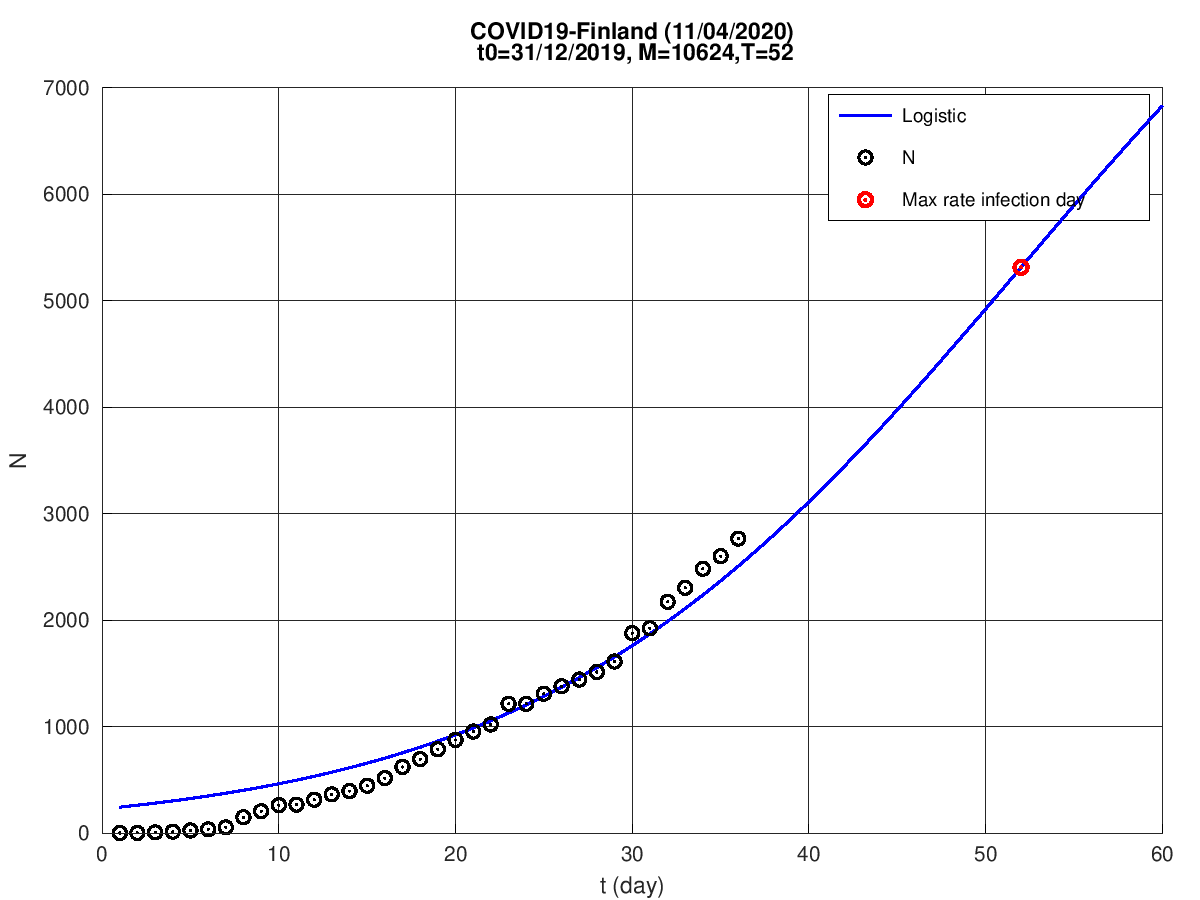
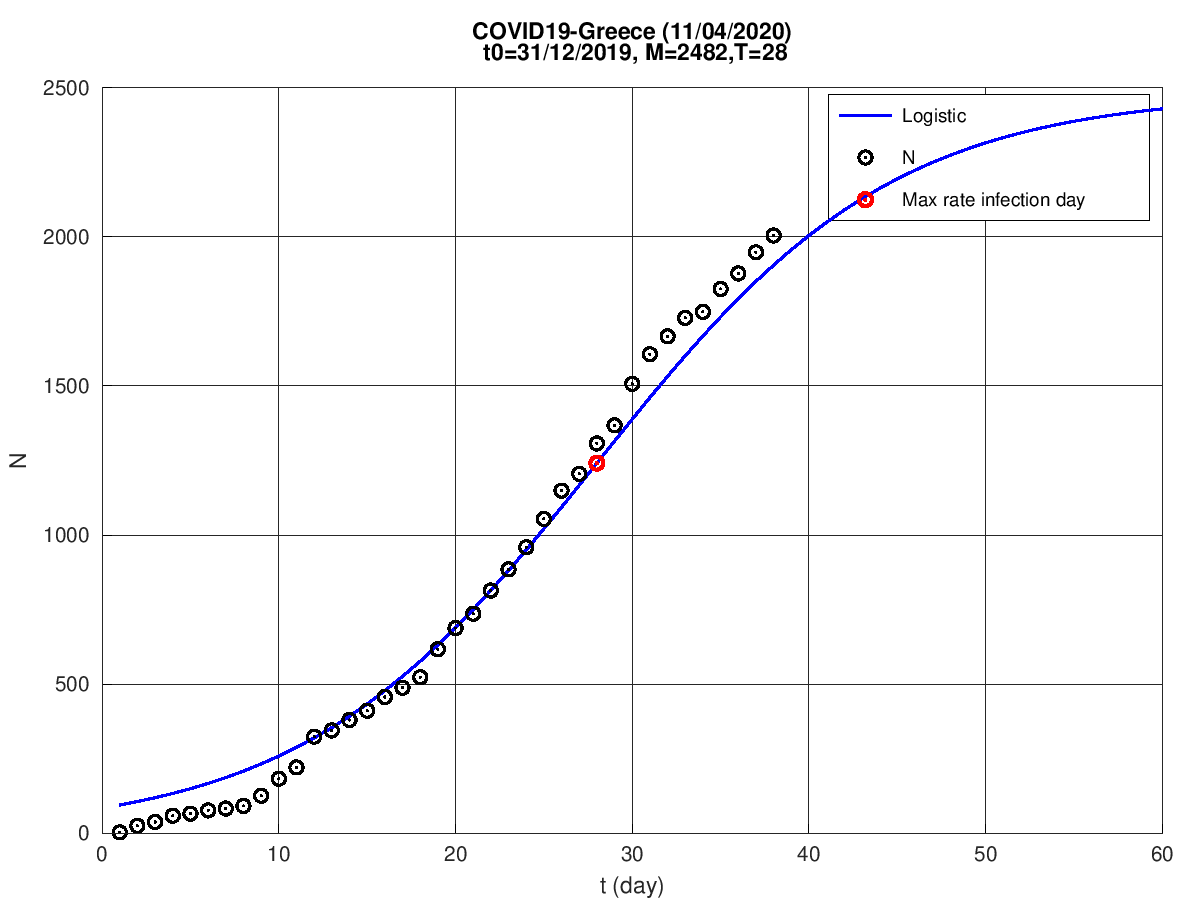
Grécia
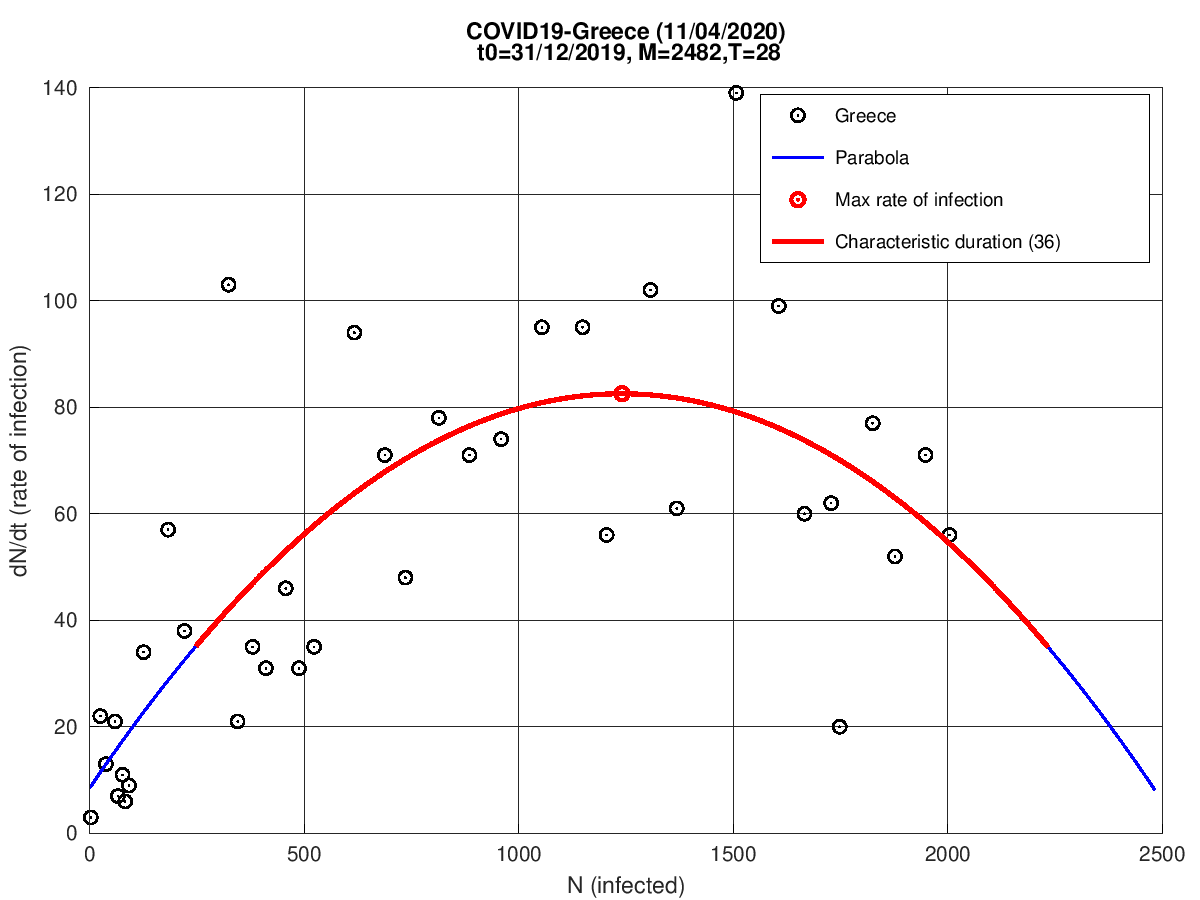
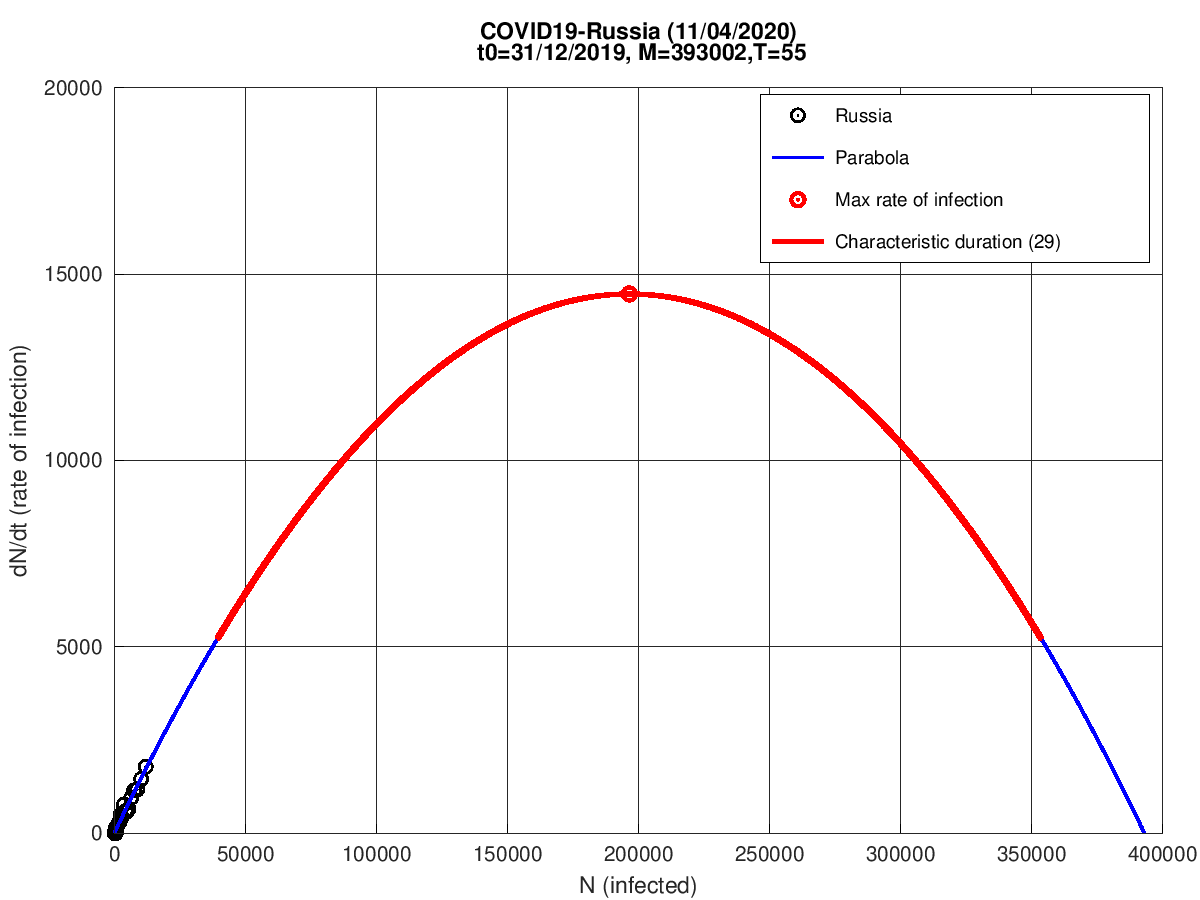
Rússia
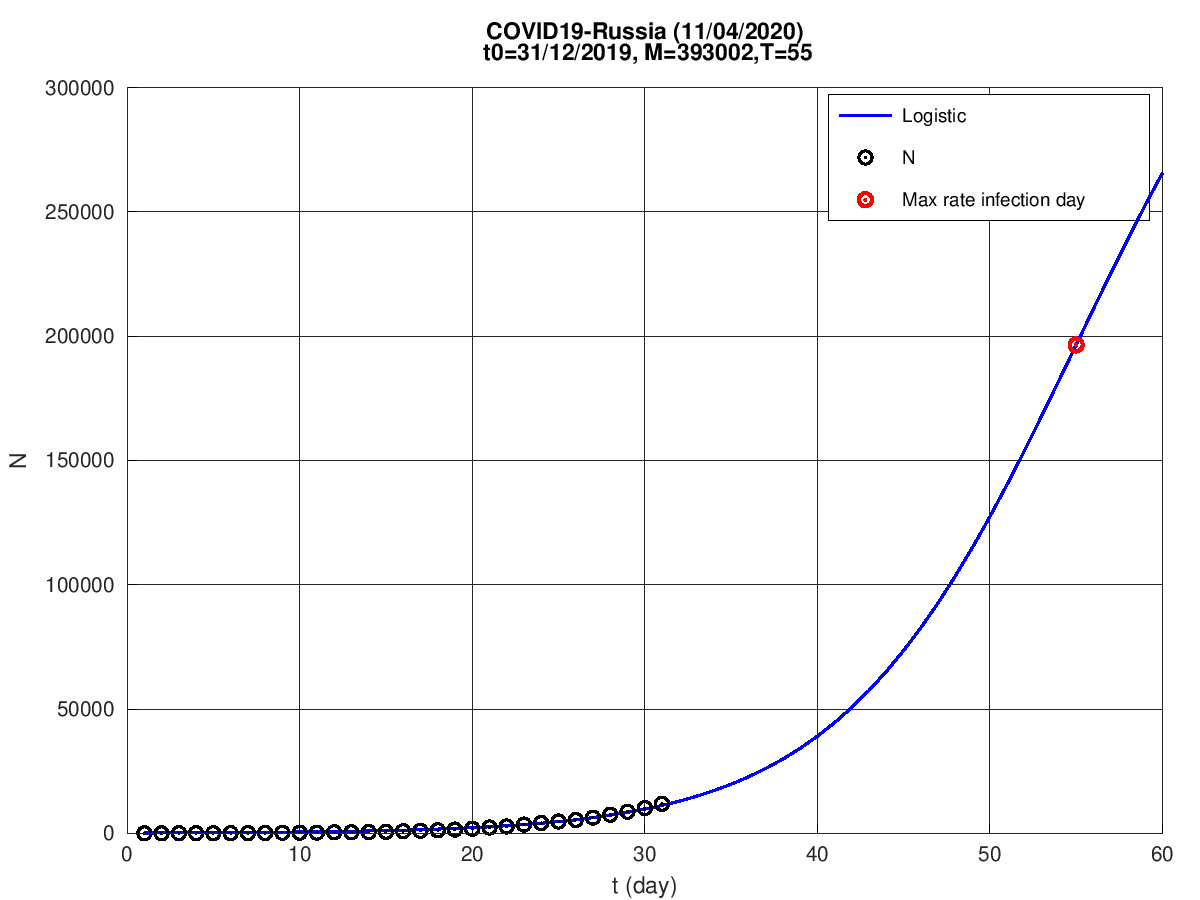
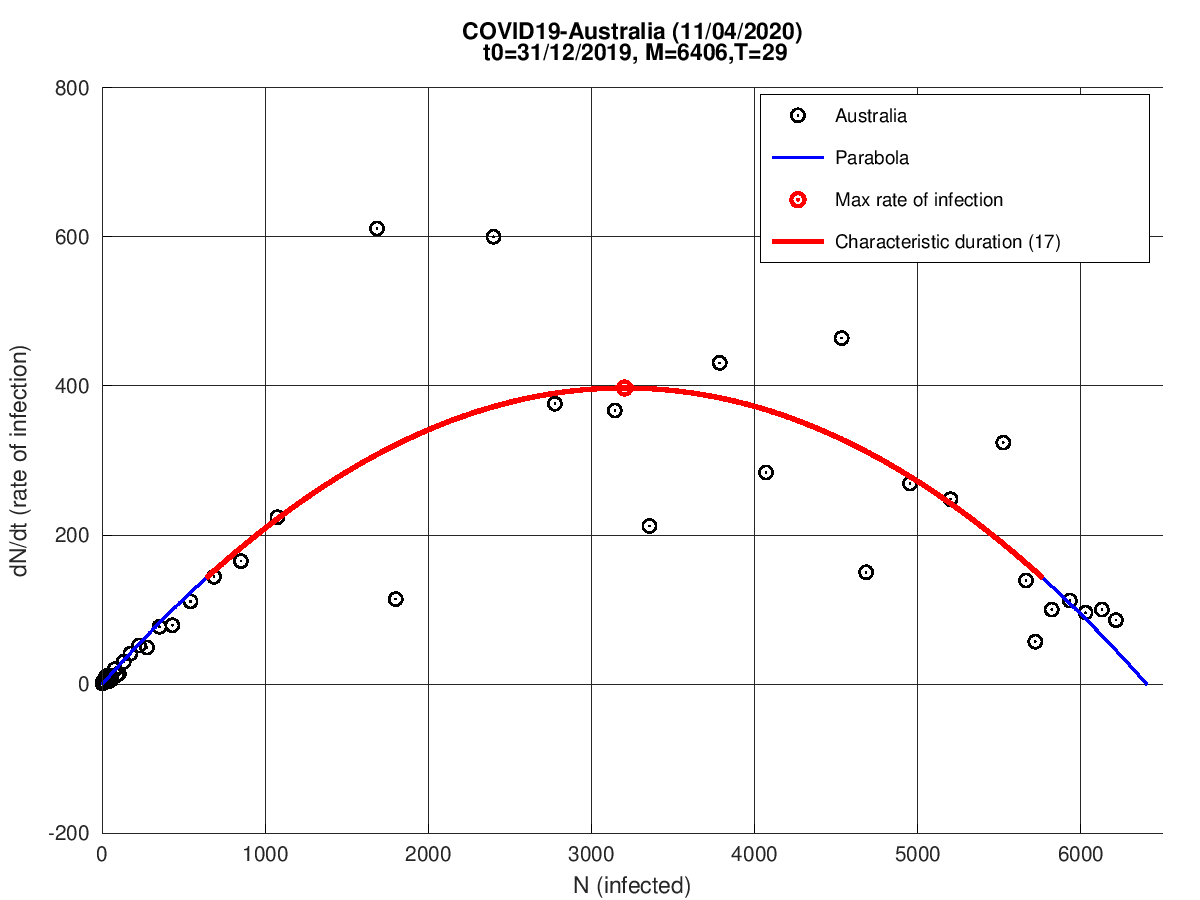
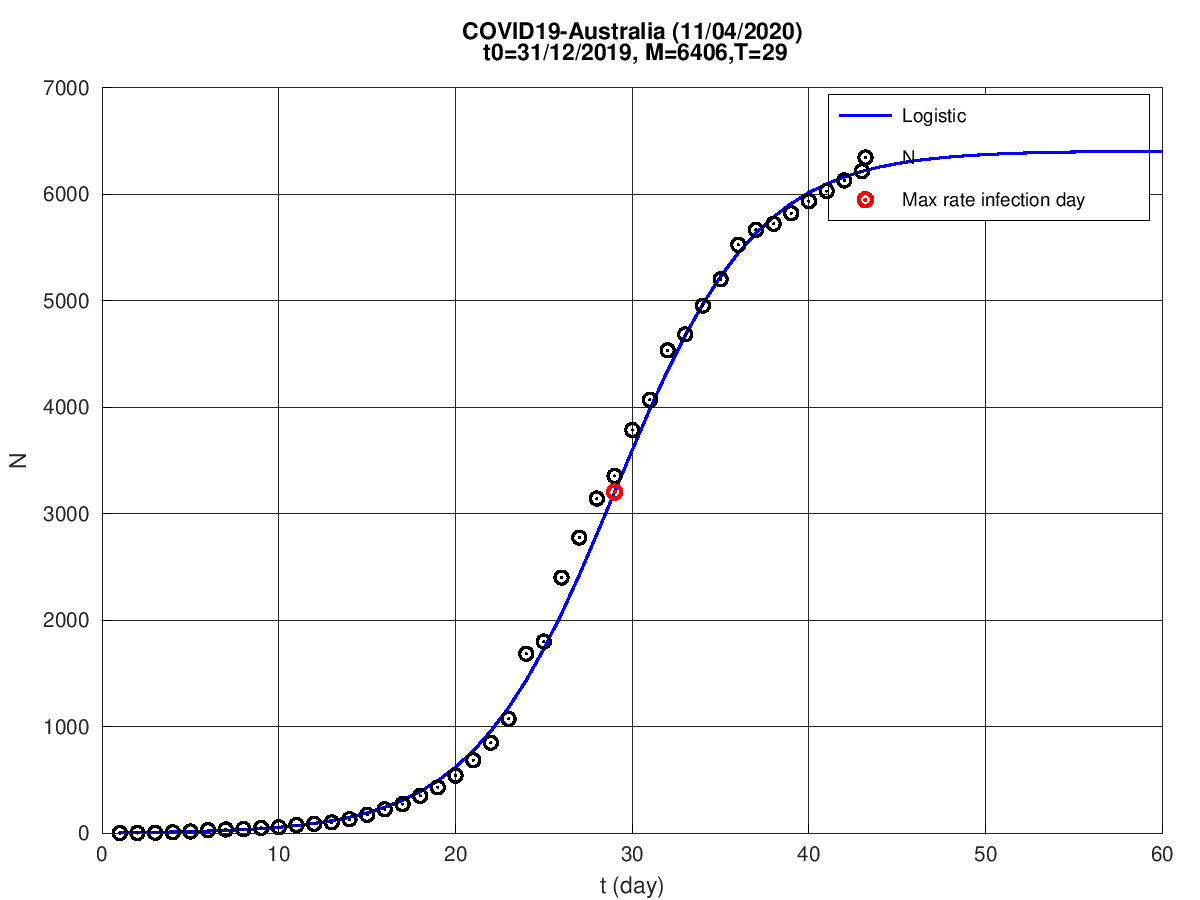
Austrália
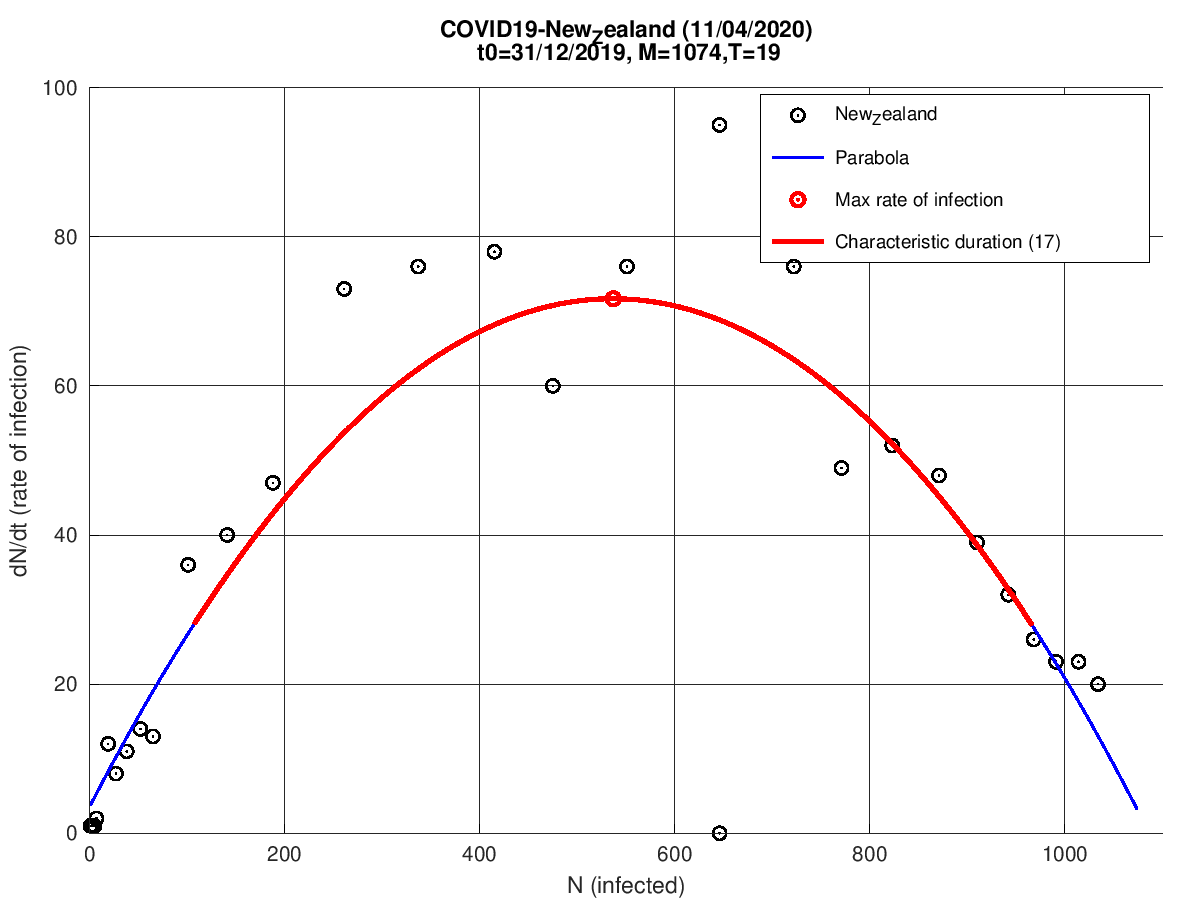
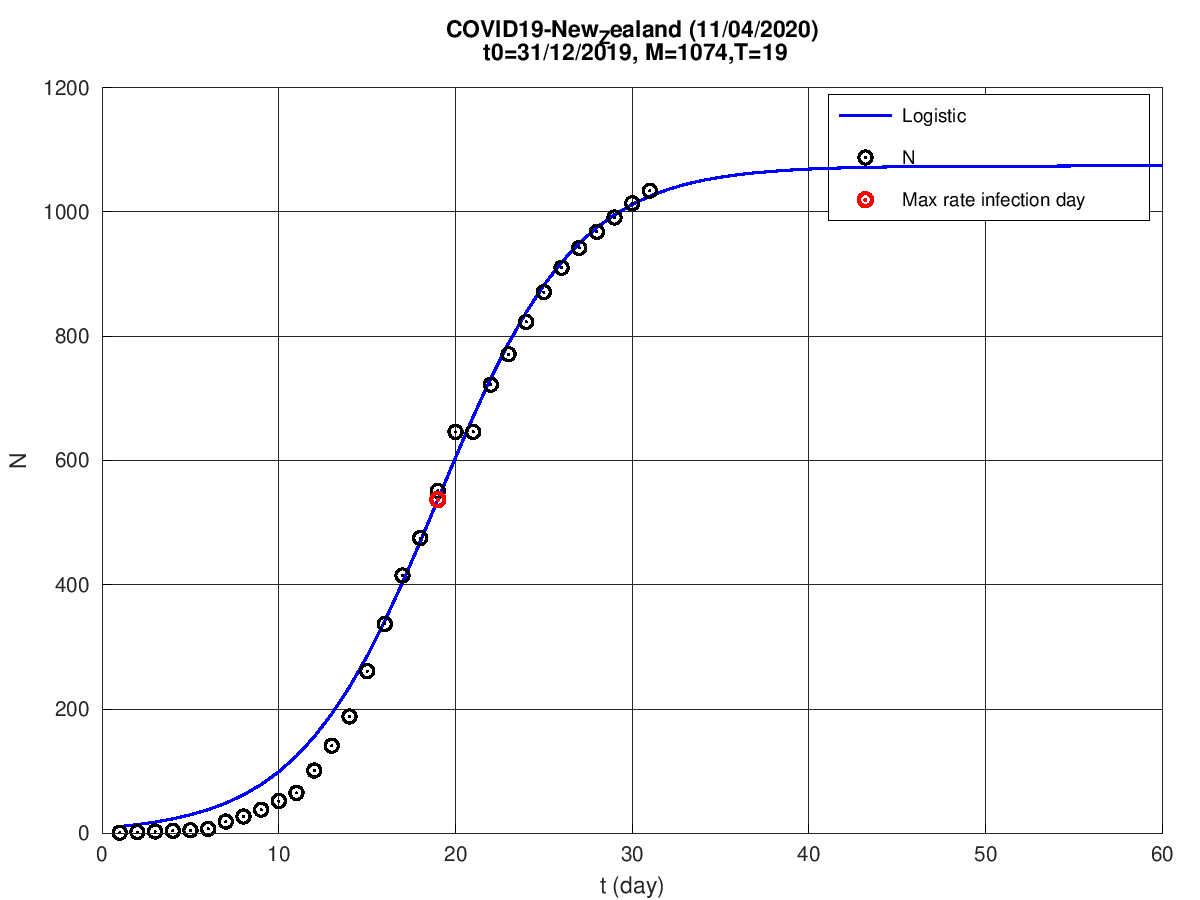
Nova Zelândia
Criado/Created: 02-04-2020 [18:41]
Última actualização/Last updated: 27-11-2024 [17:00]
For attribution, please cite this work as:
Charters, T., "Parábolas para que te quero": https://nexp.pt/ddr/datacovid.html (02-04-2020 [18:41])
(c) Tiago Charters