Parábolas e logística
Todos os dias, a meio do dia, recebemos o relatório da Direção Geral de Saúde sobre o desenvolvimento da epidemia do COVID19 em Portugal. Dois números são normalmente destacados nos órgãos de comunicação social e nas redes sociais. São eles o número total de infectados, N, e a variação desse número relativamente ao dia anterior, dN/dt. São números importantes, são duas quantidades relevantes para a descrição da propagação da epidemia porque a equação do movimento (a mais simples) epidémica relaciona estas duas quantidades.
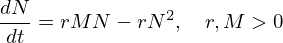
Note-se o polinómio de grau dois em N no lado direito da ODE com coeficientes rM e -r.
A solução da equação anterior com condição inicial
, 
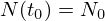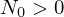é dada por
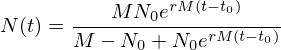
O valor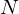 
atinge metade do valor máximo
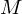no instante
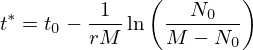
e com este valor a solução pode ser escrita de uma forma simples (tomamos to igual a zero)
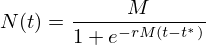
Um parâmetro relevante que mede o tempo característico da evolução da epidemia, intervalo de tempo que decorre entre 10% e 90% do número de infectados, é dado por
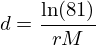
Temos então os três parâmetros a determinar: r, M, No. Como se estimam então esses parâmetros dos dados que nos são dados todos os dias?
- r e M são retirados pelo ajuste (mínimos quadrados,
c(3)+c(2)*x+c(1)x^2)) aos dados e são, respectivamente,c(1)e-c(2)/c(1); o vértice da parábola está localizado em-c(2)/(2*c(1))e-(c(2)^2-4*c(1)*c(3))/(4*c(1)).
E assim se obtém o retrato de fase da ODE da logística.
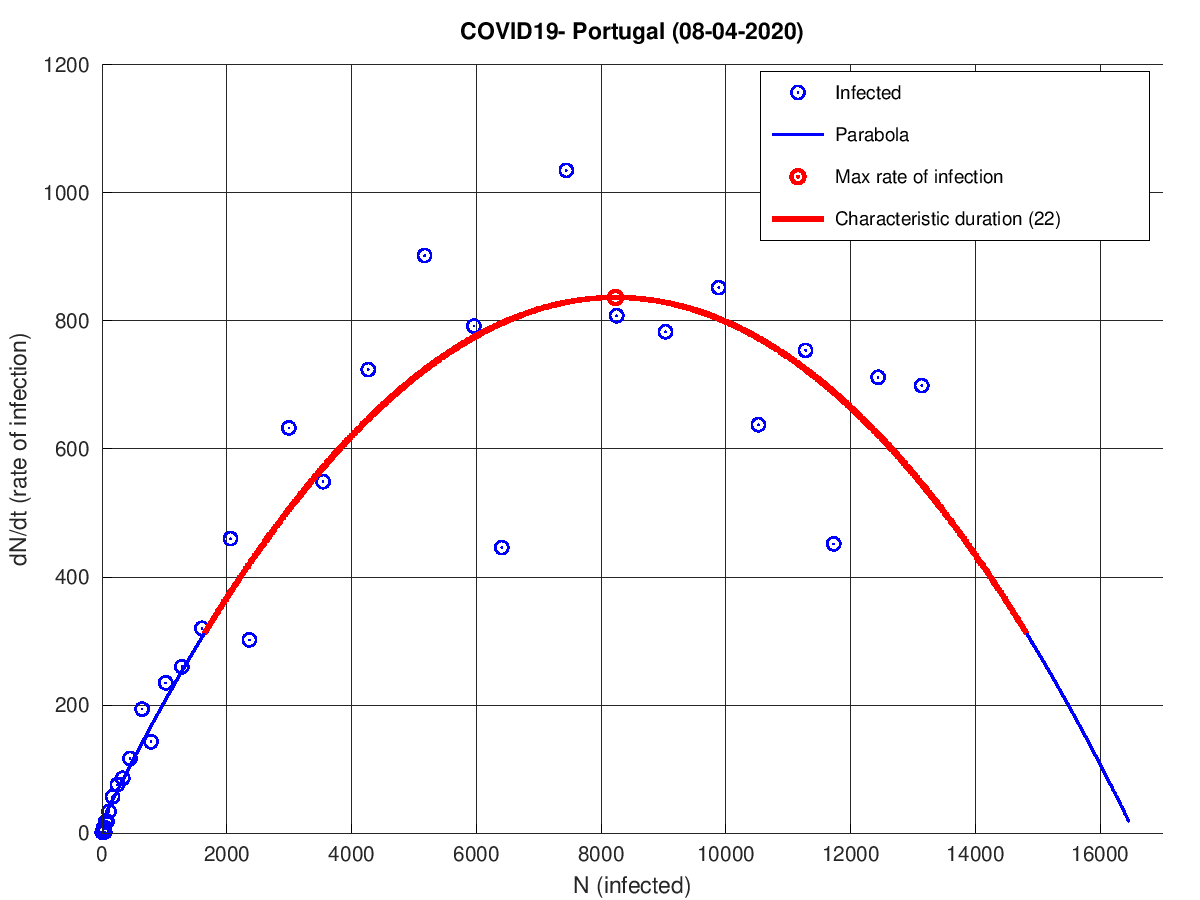
Com o procedimento anterior determinamos dois dos coeficientes. Falta-nos um, No, o número inicial de infetados (determinar No é equivalente a determinar t*). Depois de calculado podemos traçar o gráfico da solução.
Depois de terminados r e M determinamos o instante t*, turning point, o "pico" onde a taxa de infeção é máxima, minimizando a distância quadrática da função logística obtida aos dados. Este procedimento determina t* e por sua vez No (este número estimado é igual a 35).
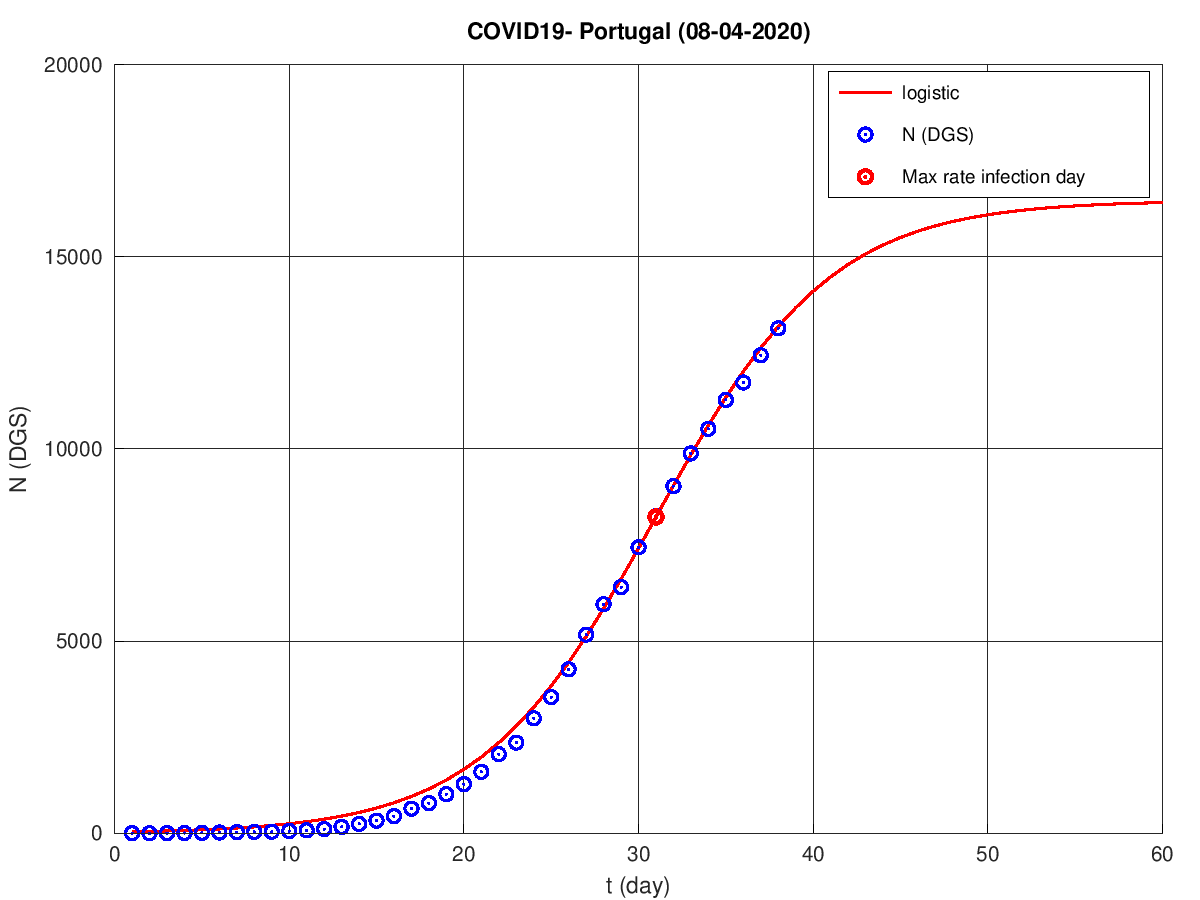
E já está.
Os gráficos anteriores foram obtidos com os dados da Direcção Geral de Saúde agrupados, para o dia 08/04/2020, pelo colectivo Data Science for Social Good Portugal e estão disponíveis para download no github da dssg-pt.
Criado/Created: 09-04-2020 [10:04]
Última actualização/Last updated: 27-11-2024 [17:00]
For attribution, please cite this work as:
Charters, T., "Parábolas e logística": https://nexp.pt/ddr/parabola.html (09-04-2020 [10:04])
(c) Tiago Charters